Einfluss von c: Unterschied zwischen den Versionen
K |
K |
||
| Zeile 13: | Zeile 13: | ||
}} | }} | ||
| + | ''Lösung:'' {{versteckt| | ||
| + | |||
| + | {{Merksatz|MERK= | ||
| + | Man erhält den Graph der Funktion | ||
| + | :<math> x \rightarrow a\cdot \sin x </math> | ||
| + | aus dem Graph der Sinusfunktion durch Streckung oder Stauchung in Richtung der <math>\ y</math>-Achse. Man sagt, die Amplitude der Funktion wird vergrößert oder verkleinert. Genauer: | ||
| + | * <span style="background-color:yellow;"> Ist der Betrag von <math>\ a</math> größer als eins, so wird der Graph der Sinusfunktion in <math>\ y</math>-Richtung um den Faktor Betrag von <math> \ a </math> gestreckt. | ||
| + | * Ist der Betrag von <math>\ a</math> kleiner als eins, so wird der Graph der Sinusfunktion in <math>\ y</math>-Richtung um den Faktor Betrag von <math> \ a </math> gestaucht. | ||
| + | * Falls <math> \ a </math> negativ ist, so wird der Graph zusätzlich an der <math>\ x</math>-Achse gespiegelt.}} | ||
| + | </span> | ||
| + | |||
| + | <graphviz> | ||
| + | digraph G { | ||
| + | rankdir=LR; | ||
| + | "Start"-> "|a| > 1"; | ||
| + | "Start"-> "|a| < 1"; | ||
| + | "|a| > 1"->"Streckung in y-Richtung \n um den Faktor a"; | ||
| + | "Streckung in y-Richtung \n um den Faktor a" -> "a > 0"; | ||
| + | "a > 0" -> "Ziel"; | ||
| + | "Streckung in y-Richtung \n um den Faktor a" -> "a < 0"; | ||
| + | "a < 0" -> "Spiegelung an \n der x-Achse"; | ||
| + | "Spiegelung an \n der x-Achse"-> "Ziel"; | ||
| + | "|a| < 1"-> "Stauchung in y-Richtung \n um den Faktor a"; | ||
| + | "Stauchung in y-Richtung \n um den Faktor a" -> "a > 0"; | ||
| + | "Stauchung in y-Richtung \n um den Faktor a" -> "a < 0"; | ||
| + | } | ||
| + | </graphviz> | ||
| + | |||
| + | }} | ||
''Lösung:'' {{versteckt| | ''Lösung:'' {{versteckt| | ||
[[Bild:N_sin_c.jpg|center]] | [[Bild:N_sin_c.jpg|center]] | ||
Version vom 7. November 2008, 20:19 Uhr
Wir betrachten nun den Einfluss von  in
in
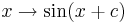 .
.
|
|
Lösung:
Lösung:
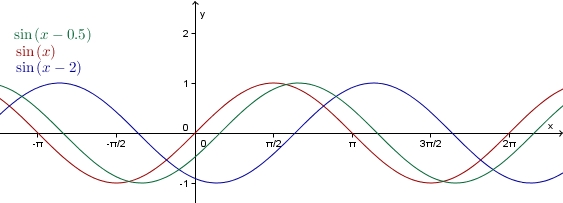
Man erhält den Graph der Funktion f: x---> sin(x+c) aus dem Graph der Sinusfunktion sin durch Verschiebung um -c in Richtung der x-Achse.
Beachte dabei:
Ist c > 0, so verschiebe um den Betrag von c nach links entlang der x-Achse;
ist c < 0, so verschiebe um den Betrag von c nach rechts entlang der x-Achse.
|
Teste Dich! Klicke auf die richtigen Zuordnungen! |
Nun betrachten wir den Einfluss von  in
in
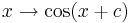 .
.
|
Öffne dieses GeoGebra-Applet und bearbeite damit obige Aufgaben eins bis vier nochmals.
|
Hefteintrag
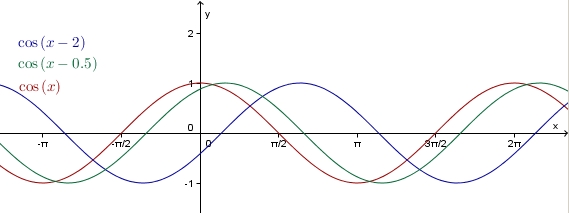
Man erhält den Graph der Funktion f: x---> sin(x+c) aus dem Graph der Kosinusfunktion cos durch Verschiebung um -c in Richtung der x-Achse.
Beachte dabei:
Ist c > 0, so verschiebe um den Betrag von c nach links entlang der x-Achse;
ist c < 0, so verschiebe um den Betrag von c nach rechts entlang der x-Achse.
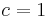 ein. Wie ändert sich der Graph?
ein. Wie ändert sich der Graph? 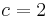 und
und 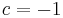 , sowie
, sowie 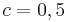 und
und 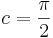 auf den Graphen auswirken und überprüfe Deine Vermutung.
auf den Graphen auswirken und überprüfe Deine Vermutung.