Einfluss von d: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
K |
K |
||
| Zeile 12: | Zeile 12: | ||
<br> | <br> | ||
}} | }} | ||
| + | |||
| + | ''Lösung:'' {{versteckt| | ||
| + | |||
| + | {{Merksatz|MERK= | ||
| + | Man erhält den Graph der Funktion | ||
| + | :<math> x \rightarrow \sin ( x + c ) </math> | ||
| + | aus dem Graph der Sinusfunktion durch Verschiebung in Richtung der <math>\ x</math>-Achse. Genauer: | ||
| + | * <span style="background-color:yellow;"> Ist <math>\ c</math> positiv, so wird der Graph der Sinusfunktion um den Betrag von <math> \ c </math> nach links verschoben. | ||
| + | * Ist <math>\ c</math> negativ, so wird der Graph der Sinusfunktion um den Betrag von <math> \ c </math> nach rechts verschoben. }} | ||
| + | </span> | ||
| + | |||
| + | <graphviz> | ||
| + | digraph G { | ||
| + | rankdir=LR; | ||
| + | "Start"-> "c > 0"; | ||
| + | "Start"-> "c < 0"; | ||
| + | "c > 0"->"Verschiebung nach links \n um den Betrag von c"; | ||
| + | "Verschiebung nach links \n um den Betrag von c" -> "Ziel"; | ||
| + | "c < 0"-> "Verschiebung nach rechts \n um den Betrag von c"; | ||
| + | "Verschiebung nach rechts \n um den Betrag von c" -> "Ziel"; | ||
| + | } | ||
| + | </graphviz> | ||
| + | [[Bild:N_sin_c.jpg|center]] | ||
| + | }} | ||
| + | |||
| + | |||
''Lösung:'' {{versteckt| | ''Lösung:'' {{versteckt| | ||
[[Bild:N_sin_d.jpg|center]] | [[Bild:N_sin_d.jpg|center]] | ||
Version vom 7. November 2008, 21:19 Uhr
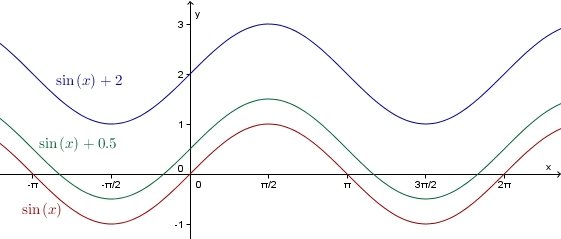
Wir betrachten nun den Einfluss von 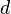 in
in
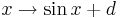 .
.
|
|
Lösung:
{{{1}}}
Lösung:
Man erhält den Graph der Funktion f: x---> sin(x)+d aus dem Graph der Sinusfunktion sin durch Verschiebung um d in Richtung der y-Achse.
|
Teste Dich! Klicke auf die richtigen Zuordnungen! |
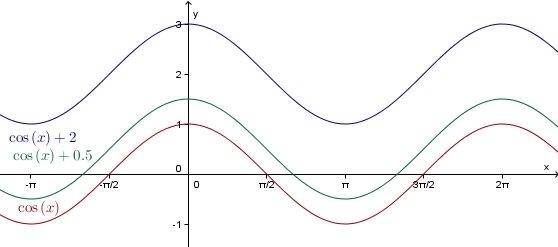
Nun betrachten wir den Einfluss von 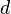 in
in
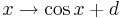 .
.
|
Öffne dieses GeoGebra-Applet und bearbeite damit obige Aufgaben eins bis vier nochmals.
|
Hefteintrag
Man erhält den Graph der Funktion f: x---> cos(x)+d aus dem Graph der Kosinusfunktion cos durch Verschiebung um d in Richtung der y-Achse.
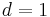 ein. Wie ändert sich der Graph?
ein. Wie ändert sich der Graph? 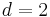 und
und 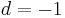 sowie
sowie 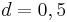 auf den Graphen auswirken und überprüfe Deine Vermutung.
auf den Graphen auswirken und überprüfe Deine Vermutung.