Potenzfunktionen - 3. Stufe: Unterschied zwischen den Versionen

Aus Medienvielfalt-Wiki
Wechseln zu: Navigation, Suche
Zeile 20: Zeile 20:
  
 
Beispiele:  
 
Beispiele:  
 +
 +
<math>\sqrt{16} = \begin{cases} 4\cdot 4\\ -4 \cdot 4 \end{cases}.</math>
 +
  
 
* <math>\sqrt[2]{16}:=\sqrt{16}=\sqrt{4\cdot 4} = \sqrt{4^2} = \sqrt{4}^2 = 4</math>, dagegen
 
* <math>\sqrt[2]{16}:=\sqrt{16}=\sqrt{4\cdot 4} = \sqrt{4^2} = \sqrt{4}^2 = 4</math>, dagegen

Version vom 19. Januar 2009, 11:58 Uhr

Start - Einführung - 1. Stufe - 2. Stufe - 3. Stufe - 4. Stufe - 5. Stufe

Die Graphen der Funktionen mit f(x) = x1/n, n ∈ IN

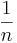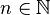Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen positiven Stammbruch der Form \frac{1}{n} mit n \in \mathbb{N} als Exponenten haben.

Potenzen und Wurzeln

Potenzfunktionen der Bauart 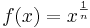f(x)=x^{\frac{1}{n}} und Wurzelfunktionen g(x)=\sqrt[n]{x} hängen eng zusammen, denn es gilt:

x^{\frac{1}{n}}:=\sqrt[n]{x}

Darin ist die n-te Wurzel festgelegt über:

\sqrt[n]{x} :\Leftrightarrow \left(\sqrt[n]{x}\right)^n = x

Beispiele:

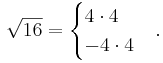
\sqrt{16} = \begin{cases} 4\cdot 4\\ -4 \cdot 4 \end{cases}.


  • \sqrt[2]{16}:=\sqrt{16}=\sqrt{4\cdot 4} = \sqrt{4^2} = \sqrt{4}^2 = 4, dagegen
  • 4\cdot4 = 16 = -4 \cdot -4 \Leftarrow \sqrt{1}
  • \sqrt[3]{27}=\sqrt[3]{3\cdot 3 \cdot 3} = \sqrt[3]{3^3} = \sqrt[3]{3}^3 = 3, aber auch
  • \sqrt[3]{-27}=\sqrt[3]{-3\cdot -3 \cdot -3} = \sqrt[3]{-3^3} = \sqrt[3]{-3}^3 = -3.

Von „http://medienvielfalt.zum.de/index.php?title=Potenzfunktionen_-_3._Stufe&oldid=1881“