Zusatzaufgaben: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
K (→Zusatzaufgaben) |
K (→Experimentier-Ecke) |
||
| Zeile 38: | Zeile 38: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[zw:Trigonometrische Funktionen]] | [[zw:Trigonometrische Funktionen]] | ||
Version vom 20. Januar 2009, 14:40 Uhr
Einführung - Einfluss der Parameter - Bestimmung der Funktionsgleichung aus dem Graphen - Anwendungen in der Physik - Zusatzaufgaben
Zusatzaufgaben
|
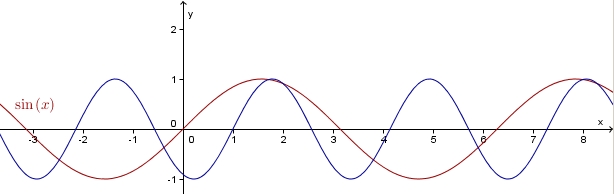
In dem unteren Bild sind der Graph der Sinusfunktion (rot) und ein weiterer Graph einer Sinusfunktion (schwarz) zu sehen.
|
a) Die Nullstellen der Sinusfunktion sind bei allen Vielfachen von PI, also x = k*PI.
b) Die Nullstellen der "schwarzen" Funktion sind bei x = 1, 1+PI/2, 1+PI, ...
c) Hochpunkte sind bei x = 1 + PI/4, 1 + 5/4*PI, ...
Tiefpunkte sind bei x = 1 - PI/4, 1 + 3/4*PI, ...
|
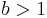 den Parameter
den Parameter  änderst?
änderst?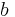 und
und 
