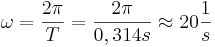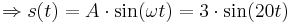Lösung zu Aufgabe P4: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(Lösung eingefügt) |
(link zurück eingefügt) |
||
| Zeile 1: | Zeile 1: | ||
| + | *[[Trigonometrische Funktionen/Anwendungen in der Physik|Zurück zu Station 3: Anwendungen in der Physik]] | ||
| + | |||
| + | ---- | ||
| + | |||
1. Die Schwingungsdauer kann sehr genau bestimmt werden, indem man zunächst zwei Nullstellen wählt, die sehr genau abgelesen werden können. | 1. Die Schwingungsdauer kann sehr genau bestimmt werden, indem man zunächst zwei Nullstellen wählt, die sehr genau abgelesen werden können. | ||
| Zeile 10: | Zeile 14: | ||
:<math>\Rightarrow s(t) = A \cdot \sin(\omega t) = 3 \cdot \sin(20t)</math> | :<math>\Rightarrow s(t) = A \cdot \sin(\omega t) = 3 \cdot \sin(20t)</math> | ||
| + | |||
| + | ---- | ||
| + | |||
| + | *[[Trigonometrische Funktionen/Anwendungen in der Physik|Zurück zu Station 3: Anwendungen in der Physik]] | ||
Version vom 27. Februar 2009, 21:30 Uhr
1. Die Schwingungsdauer kann sehr genau bestimmt werden, indem man zunächst zwei Nullstellen wählt, die sehr genau abgelesen werden können.
- Nullstellen:
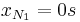 und
und 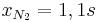
- Da in 1,1 Sekunden 3,5 Schwingungen stattfinden, erhält man als Schwingungsdauer:
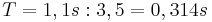
- Frequenz:
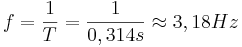
2. 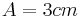 und
und 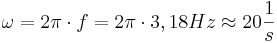 oder
oder