Lösung zu Aufgabe A1: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(link zurück eingefügt) |
(link zurück eingefügt) |
||
| Zeile 1: | Zeile 1: | ||
*[[Einfluss von a|Zurück zu Station 1: Einfluss der Parameter - Einfluss von a]] | *[[Einfluss von a|Zurück zu Station 1: Einfluss der Parameter - Einfluss von a]] | ||
| + | |||
---- | ---- | ||
| + | |||
{| | {| | ||
| | | | ||
| Zeile 44: | Zeile 46: | ||
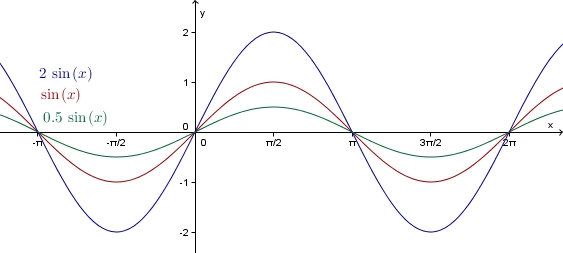
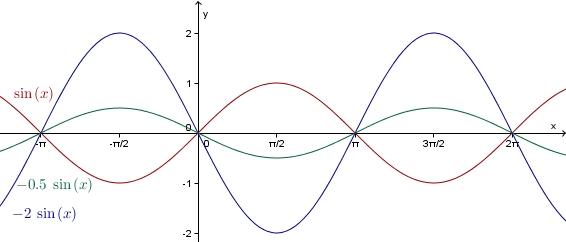
Für negative a (a < 0) muss man den Graph noch an der x-Achse spiegeln. --> | Für negative a (a < 0) muss man den Graph noch an der x-Achse spiegeln. --> | ||
[[Bild:N_sin_a-.jpg|center]] | [[Bild:N_sin_a-.jpg|center]] | ||
| + | |||
| + | ---- | ||
| + | |||
| + | *[[Einfluss von a|Zurück zu Station 1: Einfluss der Parameter - Einfluss von a]] | ||
Version vom 28. Februar 2009, 18:25 Uhr
|
<graphviz> digraph G { rankdir=LR; "Start"-> "|a| > 1"; "Start"-> "|a| < 1"; "|a| > 1"->"Streckung in y-Richtung \n mit dem Faktor |a|"; "Streckung in y-Richtung \n mit dem Faktor |a|" -> "a > 0"; "a > 0" -> "Ziel"; "Streckung in y-Richtung \n mit dem Faktor |a|" -> "a < 0"; "a < 0" -> "Spiegelung an \n der x-Achse"; "Spiegelung an \n der x-Achse"-> "Ziel"; "|a| < 1"-> "Stauchung in y-Richtung \n mit dem Faktor |a|"; "Stauchung in y-Richtung \n mit dem Faktor |a|" -> "a > 0"; "Stauchung in y-Richtung \n mit dem Faktor |a|" -> "a < 0"; } </graphviz>

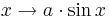
 -Achse. Genauer:
-Achse. Genauer:
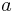 größer als eins, so wird der Graph der Sinusfunktion in
größer als eins, so wird der Graph der Sinusfunktion in 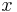 -Achse gespiegelt.
-Achse gespiegelt.