Quadratische Funktionen - Übungen 3: Unterschied zwischen den Versionen
(ergänzung) |
(hilfe ergänzt) |
||
| Zeile 66: | Zeile 66: | ||
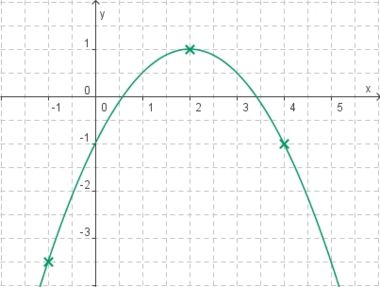
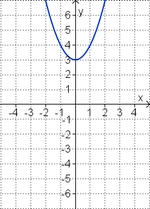
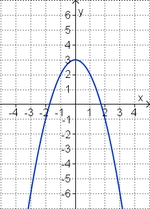
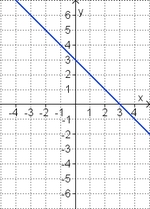
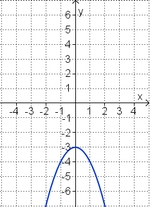
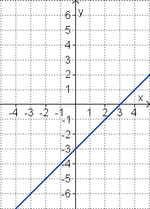
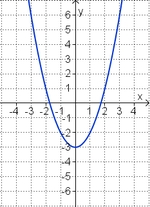
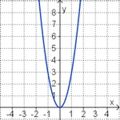
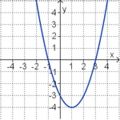
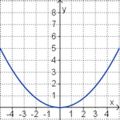
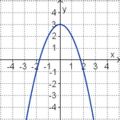
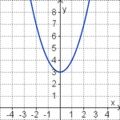
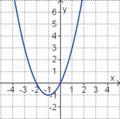
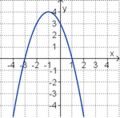
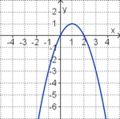
<big>'''Übung 4: Memo-Quiz'''</big> | <big>'''Übung 4: Memo-Quiz'''</big> | ||
| − | Finde die richtigen Paare - je ein Funktionsterm und ein Funktionsgraph gehören zusammen. Achte auf die wesentlichen Eigenschaften der Funktion. | + | Finde die richtigen Paare - je ein Funktionsterm und ein Funktionsgraph gehören zusammen. Achte auf die wesentlichen Eigenschaften der Funktion (Öffnung der Parabel, Lage des Scheitels, Nullstellen). |
:::{|border="0" cellspacing="0" cellpadding="4" | :::{|border="0" cellspacing="0" cellpadding="4" | ||
Version vom 26. März 2009, 20:07 Uhr
Einführung - Bremsweg - Unterschiedliche Straßenverhältnisse - Übungen 1 - Anhalteweg - Übungen 2 - Allgemeine quadratische Funktion - Übungen 3 - Abschlusstest
Übung 1: Funktionsterm finden
Übung 2: Term und Graph zuordnen Ordne den Funktionsgraphen den richtigen Term zu.
-x2 + 3-x + 3-x2 - 3x2 + 3x2 - 3x - 3
Übung 3: Multiple Choice Kreuze jeweils alle richtigen Aussagen an. f(x) = –2x2 + 3x – 4
Übung 4: Memo-Quiz Finde die richtigen Paare - je ein Funktionsterm und ein Funktionsgraph gehören zusammen. Achte auf die wesentlichen Eigenschaften der Funktion (Öffnung der Parabel, Lage des Scheitels, Nullstellen).
|
