Potenzfunktionen - 4. Stufe: Unterschied zwischen den Versionen
K (→Zusammenfassung) |
K (→*Zum Weiterdenken: Mit Funktionen malen) |
||
| Zeile 140: | Zeile 140: | ||
[[Bild:rosette_2.png|thumb|frameless|right|250px|Wie müssen die Parameter verändert werden, wenn sie das Blatt links unten bilden sollen? ]] | [[Bild:rosette_2.png|thumb|frameless|right|250px|Wie müssen die Parameter verändert werden, wenn sie das Blatt links unten bilden sollen? ]] | ||
[[Bild:rosette_3.png|thumb|frameless|right|250px| Wie kann man die Größe der Blätter beeinflussen?]] | [[Bild:rosette_3.png|thumb|frameless|right|250px| Wie kann man die Größe der Blätter beeinflussen?]] | ||
| + | |} | ||
| + | |||
| + | ---- | ||
| + | {|border="0" cellspacing="0" cellpadding="4" | ||
| + | |align = "left" width="120"|[[Bild:Maehnrot.jpg|100px]] | ||
| + | |align = "left"|'''Und nun gehts zum Abschlusstest'''<br /> | ||
| + | [[Bild:Pfeil.gif]] [[Potenzfunktionen_Test|'''Hier geht es weiter''']]'''.''' | ||
| + | |||
|} | |} | ||
Version vom 28. März 2009, 18:03 Uhr
Inhaltsverzeichnis |
Die Graphen der Funktionen mit f(x) = x-1/n, n ∈ IN
Es sei stets 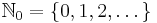 und
und 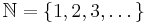 , insbesondere also
, insbesondere also 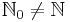 .
.
Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen negativen Stammbruch der Form 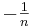 mit
mit 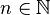 als Exponenten haben. Für diese Art der Exponenten gilt:
als Exponenten haben. Für diese Art der Exponenten gilt: 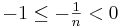 .
.
Vergleich mit Funktionen aus Stufe 3
|
Verleiche den neuen Graphen (blau) mit dem, den Du schon aus Stufe 3 dieses Kurses kennst (rot gestrichelt); mit dem Schieberegler kannst Du dazu wieder die Exponenten verändern.
|
Exponenten, Brüche und Potenzgesetze
Im vorliegenden Fall betrachten wir negative Stammbrüche als Exponenten. Denke dabei insbesondere an folgenden Zusammenhang:
- Für eine reelle Zahl
 und eine natürliche Zahl
und eine natürliche Zahl 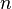 wird definiert:
wird definiert:
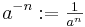 für
für 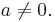
Auf unsere Situation angewandt ergibt sich:
|
Potenzfunktionen und ihre Umkehrfunktionen
Beispiel
Es sei 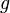 eine Potenzfunktion, definiert durch eine Potenzfunktion, definiert durch 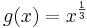 . Gesucht ist die Umkehrfunktion . Gesucht ist die Umkehrfunktion 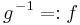 von von  . .
Vertauschen von |
Beispiel
Es sei  eine Potenzfunktion, nun definiert durch eine Potenzfunktion, nun definiert durch 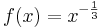 mit Definitionsbereich ID = IR+. Gesucht ist wieder ihre Umkehrfunktion mit Definitionsbereich ID = IR+. Gesucht ist wieder ihre Umkehrfunktion 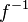 . .
Auflösen nach |
Hinweis: Man beachte besonders hier die unterschiedliche Bedeutung von 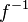 und
und 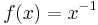 !
!
Vergleich mit Potenzfunktionen der Stufe 1
Im Zusammenhang mit den Umkehrfunktionen dieser Art kann es sinnvoll sein, sich die Potenzfunktionen der Stufe 1 noch einmal vor Augen zu führen. Hier kannst Du direkt zur Stufe 1 springen.
Zusammenfassung
Die Umkehrfunktionen von Potenzfunktionen mit 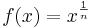 für
für 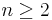 sind Potenzfunktionen mit
sind Potenzfunktionen mit 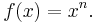
Die Umkehrfunktionen von Potenzfunktionen mit 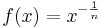 für
für 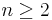 sind Potenzfunktionen mit
sind Potenzfunktionen mit 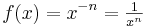 .
.
|
Zu welchen vorgegebenen Potenzfunktionen gibt es eine Umkehrfunktion? Welche Eigenschaften muss die gegebene Potenzfunktion erfüllen, damit es eine Umkehrfunktion gibt?
Potenzfunktionen mit
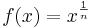 mit mit 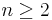 sind auf ihrem Definitionsbereich sind auf ihrem Definitionsbereich 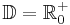 streng monoton steigend. Deswegen gibt es auf diesem Bereich eine Umkehrfunktion und zwar von der Bauart streng monoton steigend. Deswegen gibt es auf diesem Bereich eine Umkehrfunktion und zwar von der Bauart 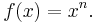 Hat man aber eine Potenzfunktion 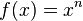 mit mit 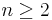 (also eine aus der Stufe 1 dieses Lernpfades) vorgegeben, so ist sie auf ihrem Defintionsbereich (also eine aus der Stufe 1 dieses Lernpfades) vorgegeben, so ist sie auf ihrem Defintionsbereich 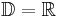 sowohl monoton fallend als auch monoton steigend. Die Umkehrbarkeit ist aber nur auf streng monotonen Intervallen möglich. Betrachtet man sowohl monoton fallend als auch monoton steigend. Die Umkehrbarkeit ist aber nur auf streng monotonen Intervallen möglich. Betrachtet man  auf dem eingeschränkten Definitionsbereich auf dem eingeschränkten Definitionsbereich 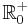 , auf dem sie streng monoton ist, dann ist sie dort umkehrbar und hat die Umkehrfunktion , auf dem sie streng monoton ist, dann ist sie dort umkehrbar und hat die Umkehrfunktion 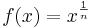 . . |
*Zusammenfassung: Was bewirken Parameter in Potenzfunktionen? - Merkregel "5 S"-Prinzip
*: freiwillig
|
Die "5 S" lauten:
Schau Dir dieses Video (Link hier) auf www.oberprima.com an und beantworte dann die folgenden Fragen:
|
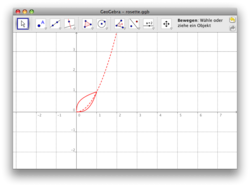
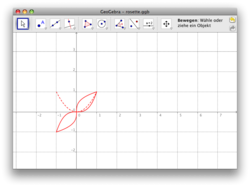
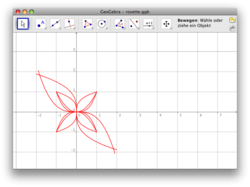
*Zum Weiterdenken: Mit Funktionen malen
(freiwillig)
|
Das obenstehende Bild ist vollständig aus Potenzfunktionen der Form mit
|
|

|
Und nun gehts zum Abschlusstest |
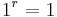 für alle
für alle 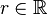 ). Der Wertebereich der blauen Graphen ist ]0,∞[.
). Der Wertebereich der blauen Graphen ist ]0,∞[.
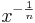
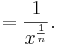
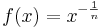 den Definitonsbereich D = IR+.
den Definitonsbereich D = IR+.
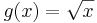 nur auf IR+o definiert, das heißt ihr Definitionsbereich
nur auf IR+o definiert, das heißt ihr Definitionsbereich 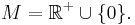
![f(x) = x^{-\frac 1 n}= \textstyle \frac{1}{x^{\frac 1 n}} = \textstyle \frac{1}{\sqrt[n]{x}} = \textstyle \frac{1}{g(x)}](/images/math/d/f/f/dffb5aedde565c318a02642cbcd56b38.png) überträgt sich der Definitionsbereich der Funktion g auf die Funktion f.
überträgt sich der Definitionsbereich der Funktion g auf die Funktion f.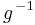 ergibt sich aus
ergibt sich aus  . Es ist:
. Es ist: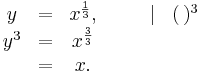
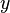 ergibt schließlich die gesuchte Funktion:
ergibt schließlich die gesuchte Funktion: 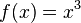 .
.
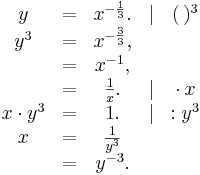
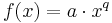
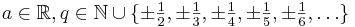 zusammengesetzt.
zusammengesetzt.