Perlenmodell und Kompetenzen: Unterschied zwischen den Versionen

Aus Medienvielfalt-Wiki
Wechseln zu: Navigation, Suche
K (Formelsatz verbessert)
 
(Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt)
Zeile 97: Zeile 97:
 
| valign="top"|
 
| valign="top"|
 
*Definitionsmenge angeben
 
*Definitionsmenge angeben
−
*Gebrochenrationale Funktionen des Typs <math>f(x) = \frac{k}{x} </math> und <math>f(x) = \frac{k}{x^2} </math> graphisch darstellen und die Graphen im Kontext interpretieren
+
*Gebrochenrationale Funktionen des Typs <math>f(x) = \textstyle \frac{k}{x} </math> und <math>f(x) = \textstyle \frac{k}{x^2} </math> graphisch darstellen und die Graphen im Kontext interpretieren
 
*Asymptoten beschreiben und im Kontext interpretieren
 
*Asymptoten beschreiben und im Kontext interpretieren
 
|}
 
|}
Zeile 198: Zeile 198:
 
| valign="top" width="3%"|
 
| valign="top" width="3%"|
 
| valign="top"|
 
| valign="top"|
−
*Integrieren als Umkehrung zum Differenzieren
+
 
  
 
|}
 
|}

Aktuelle Version vom 29. März 2009, 20:01 Uhr

Lernpfade
Intuitive Zustandsbeschreibung voneinander abhängiger Größen
  • Wortformel und intuitiver Umgang mit Tabellen und Graphen bei empirischen Funktionen, Beispiel:Wetter


Zielkompetenzen
  • Werte aus graphischen Darstellungen ablesen, sie in tabellarischer Form darstellen und im Kontext deuten
  • Zwischen den Darstellungsformeln Graph, Tabelle und Wortformel wechseln
  • Daten sammeln und in Form von Tabellen und Graphen darstellen
  • Über verschiedene Interpretationen kommunizieren können und Vergleiche anstellen
  • Ergebnisse bewerten und begründen


Zustandsbeschreibung abhängiger Größen durch Formeln
  • Umgang mit Proportionalitäten (direkt und indirekt)
(Walter K., Anita D., Irma)
  • Eigenschaften von direkter und indirekter Proportionalität beschreiben
  • Proportionalitäten in Tabellen und Graphen darstellen
  • Formeln als neue Darstellungsform verwenden
  • Modellenstscheidung (direkt, indirekt, weder noch) begründen
  • geeignete Lösungswege beim Lösen verschiedener Probleme auswählen und über die Auswahl diskutieren


Erweiterung des Repertoires an Funktionstypen und Eigenschaften
  • Umgang mit linearen Funktionen
  • Parameter variieren und Auswirkungen dieser Variationen beschreiben
  • von der graphischen Darstellung unmittelbar auf die Darstellung als Formel schließen
  • Eigenschaften linearer Funktionen aus der Termdarstellung ablesen und sie begründen (z.B.monoton steigend...)
  • Lösung linearer Gleichungssysteme in zwei Variablen als Schnittpunkte der Graphen linearer Funktionen ermitteln


  • Intuitiver Umgang mit exponentiellem Wachstum (Helmut..)
  • Übersetzen realer Situationen in mathematische Modelle (Tabellen, Graphen, Terme)
  • Die Grundeigenschaft "zu gleichen Zeitintervallen gehört der gleiche Wachstumsfaktor" exponentiellen Wachstums aus Tabellen und verbalen Formulierungen entwickeln und diese Grundeigenschaften zum Problemlösen verwenden
  • exponentielles Wachstum in Form von Tabellen rekursiv beschreiben und darstellen
  • die Eigenschaften exponentiellen und linearen Wachstums vergleichen


  • quadratische Funktionenen (Reinhard Schmidt, Maria E., Gabi J., Andrea S.)
  • Parameter variieren und Auswirkungen dieser Variationen beschreiben
  • Eigenschaften quadratischer Funktionen (Extremwerte, Symmetrie, Nullstellen) beschreiben und mit Hilfe geeigneter Darstellungsformen begründen
  • Lösungsfälle quadratischer Gleichungen mit Hilfe der Graphen quadratischer Funktionen visualisieren
  • Das Lösen quadratischer Gleichungen und Ungleichungen funktional betrachten


  • Wurzelfunktionen
  • Wurzelfunktionen als Umkehrfunktionen der quadratischen Funktionen beschreiben
  • Eigenschaften angeben und beschreiben


  • Intuitiver Umgang mit gebrochen-rationalen Funktionen
  • Definitionsmenge angeben
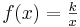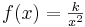  • Gebrochenrationale Funktionen des Typs f(x) = \textstyle \frac{k}{x} und f(x) = \textstyle \frac{k}{x^2} graphisch darstellen und die Graphen im Kontext interpretieren
  • Asymptoten beschreiben und im Kontext interpretieren


  • Potenzfunktionen
  • Parameter variieren und Auswirkungen dieser Variationen beschreiben
  • die Erweiterung des Potenzbegriffs (Exponent aus N, Z, Q) erklären
  • Wurzelfunktion als Potenzfunktion erkennen
  • Umkehrfunktionen als Potenzfunktionen ermitteln


  • trigonometrische Funktionen
  • Parameter variieren und die Auswirkungen dieser Variationen beschreiben
  • Eigenschaften trigonometrische Funktionen beschreiben und mit Hilfe geeigneter Darstellungsformen begründen


  • Exponential- und Logarithmusfunktionen (Gabi J., Anita D.)
  • Parameter variieren und Auswirkungen dieser Variationen beschreiben
  • Eigenschaften von Exponential- und Logarithmusfunktionen beschreiben und mit Hilfe geeigneter Darstellungsformen begründen
  • Exponential- und Logarithmusfunktionen als Umkehrfunktion kennen


  • Diskrete Wahrscheinlichkeitsverteilungsfunktionen
  • Punktgraphen im Sinne der Wahrscheinlichkeit interpretieren
  • Histogramme...???


Beschreibung der Veränderungen von Zuständen
  • diskret (Walter W, H.-G.-Weigand,)
  • Den Differenzenquotienten als diskretes Änderungsmaße kennen und darüber kommunizieren
  • Folgen als Funktionen kennen und in verschiedenen Darstellungsformen beschreiben
  • Differenzengleichungen als neuen Prototyp kennen und zur Modellbildung nutzen
  • einen intuitiven Grenzwertbegriff entwickeln und verwenden


Beschreibung der Veränderungen von Zuständen
  • kontinuierlich
  • Den Differentialquotient als kontinuierliches Änderungsmaß kennen und darüber kommunizieren
  • Den Diffentialquotienten in unterschiedlichen Anwendungssituationen erkennen und beim Problemlösen anwenden
  • Ableitungsfunktion als Hilfe beim Problemlösen verwenden (Extremwertaufgaben)
  • Differentialgleichungen als neuen Prototyp kennen und zur Modellbildung nutzen


Beschreibung durch Aufsummation
  • Flächeninhaltsfunktion
  • Unterschiedliche Methoden der Flächenberechnung kennen
  • Flächeninhalte und Funktionsgraphen näherungsweise angeben
  • die Flächeninhaltsfunktion (Abhängigkeit der oberen Grenze ....


  • Stammfunktion
  • Integrieren als Umkehrung zum Differenzieren


  • kontinuierliche Wahrscheinlichkeitsfunktion


Von „http://medienvielfalt.zum.de/index.php?title=Perlenmodell_und_Kompetenzen&oldid=3644“