Lösung zu Aufgabe C2: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(Lösung eingefügt) |
K (→Lösung zu Aufgabe C2) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Eine mögliche Begründung: | + | *[[Einfluss von c|Zurück zu Station 1: Einfluss der Parameter - Einfluss von c]] |
| + | |||
| + | ---- | ||
| + | |||
| + | ===Lösung zu Aufgabe C2=== | ||
| + | |||
| + | Hier genügt es, wenn du diese Aufgabe mit Hilfe von Plausibilitätsüberlegungen gelöst hast. Eine formale Begründung war nicht notwendig. | ||
| + | |||
| + | |||
| + | Eine mögliche formale Begründung: | ||
<math>\ \sin( x + c )=0 </math> | <math>\ \sin( x + c )=0 </math> | ||
| Zeile 8: | Zeile 17: | ||
Die Bestimmung der Nullstellen von <math> x \rightarrow \sin ( x + c ) </math> und Vergleich mit den Nullstellen der Sinuskurve zeigt, dass jeder Funktionswert für <math>\ c > 0 </math> bereits ein Stück weiter links angenommen wird. Genauer, der Graph wird also für <math>\ c > 0</math> um <math>\ c </math> nach links verschoben und für <math>\ c < 0 </math> entsprechend nach rechts. | Die Bestimmung der Nullstellen von <math> x \rightarrow \sin ( x + c ) </math> und Vergleich mit den Nullstellen der Sinuskurve zeigt, dass jeder Funktionswert für <math>\ c > 0 </math> bereits ein Stück weiter links angenommen wird. Genauer, der Graph wird also für <math>\ c > 0</math> um <math>\ c </math> nach links verschoben und für <math>\ c < 0 </math> entsprechend nach rechts. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | *[[Einfluss von c|Zurück zu Station 1: Einfluss der Parameter - Einfluss von c]] | ||
Aktuelle Version vom 9. Juli 2009, 17:34 Uhr
Lösung zu Aufgabe C2
Hier genügt es, wenn du diese Aufgabe mit Hilfe von Plausibilitätsüberlegungen gelöst hast. Eine formale Begründung war nicht notwendig.
Eine mögliche formale Begründung:
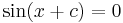
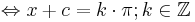
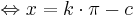
Die Bestimmung der Nullstellen von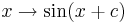 
und Vergleich mit den Nullstellen der Sinuskurve zeigt, dass jeder Funktionswert für 
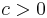bereits ein Stück weiter links angenommen wird. Genauer, der Graph wird also für 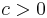um 
nach links verschoben und für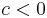 
entsprechend nach rechts.
