Quadratische Funktionen - Übungen 3: Unterschied zwischen den Versionen
| Zeile 118: | Zeile 118: | ||
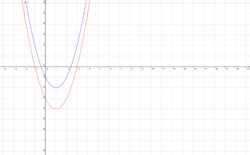
a)<center> Verschiebung in y- Richtung: | a)<center> Verschiebung in y- Richtung: | ||
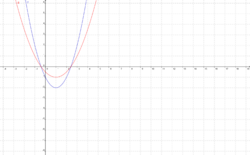
Die Form bleibt erhalten, der y- Wert des Scheitels ändert sich. Die Achsenschnittpunkte ändern sich. <br /> | Die Form bleibt erhalten, der y- Wert des Scheitels ändert sich. Die Achsenschnittpunkte ändern sich. <br /> | ||
| − | + | ||
[[Bild:nator1.png|250px]]<br /> | [[Bild:nator1.png|250px]]<br /> | ||
| + | f(x) ist die blaue Funktion, g(x) stellt die rote, in y- Richtung verschobene Funktion dar. | ||
b) Streckung in y- Richtung: | b) Streckung in y- Richtung: | ||
Schnittpunkte mit der x- Achse bleiben unverändert. Die Form und der y- Wert des Scheitelpunktes ändert sich. Schnittpunkt mit der y- Achse ändert sich. <br /> | Schnittpunkte mit der x- Achse bleiben unverändert. Die Form und der y- Wert des Scheitelpunktes ändert sich. Schnittpunkt mit der y- Achse ändert sich. <br /> | ||
| + | |||
| + | [[Bild:nator2.png|250px]]<br /> | ||
f(x) ist die blaue Funktion, g(x) stellt die rote, in y- Richtung gestreckte Funktion dar. | f(x) ist die blaue Funktion, g(x) stellt die rote, in y- Richtung gestreckte Funktion dar. | ||
| − | |||
}} | }} | ||
Version vom 14. März 2010, 19:38 Uhr
Einführung - Bremsweg - Unterschiedliche Straßenverhältnisse - Übungen 1 - Anhalteweg - Übungen 2 - Stationenbetrieb - Allgemeine quadratische Funktion - Übungen 3
Aufgabe 1: Funktionsterm finden
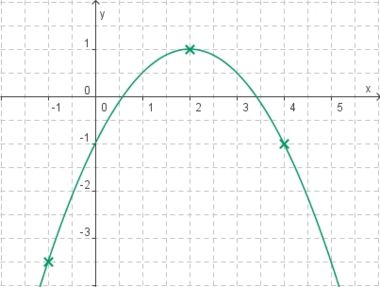
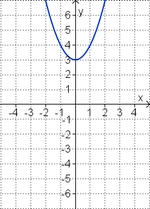
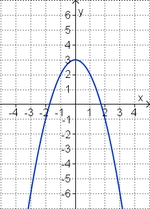
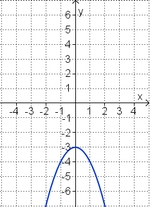
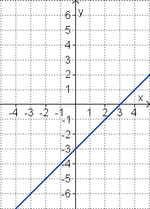
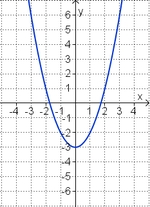
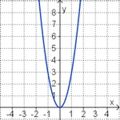
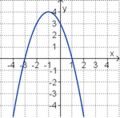
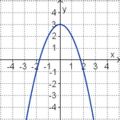
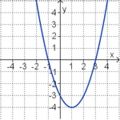
Aufgabe 2: Term und Graph zuordnen Ordne den Funktionsgraphen den richtigen Term zu.
Aufgabe 3: Multiple Choice Kreuze jeweils alle richtigen Aussagen an. f(x) = –2x2 + 3x – 4
Aufgabe 4: Memo-Quiz Finde die richtigen Paare - je ein Funktionsterm und ein Funktionsgraph gehören zusammen. Achte auf die wesentlichen Eigenschaften der Funktion (Öffnung der Parabel, Lage des Scheitels, Nullstellen). Aufgabe 5: Verschiebung und Streckung
a) in y- Richtung verschoben und b) in y- Richtung gestreckt.
|