Quadratische Funktionen - Übungen 2: Unterschied zwischen den Versionen
(kopfzeile) |
K (hat „Quadratische Funktionen - Übungen2“ nach „Quadratische Funktionen - Übungen 2“ verschoben: typo) |
||
| (8 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Quadratische Funktionen}} | |
| − | + | ||
| − | + | ||
| + | <center><span style="background:#FFFACD">Falls es Probleme mit der Ansicht gibt, bitte [[:zw:Firefox|Firefox]] als Browser verwenden!</span></center> | ||
{| | {| | ||
Aktuelle Version vom 4. Januar 2011, 12:42 Uhr
Einführung - Bremsweg - Unterschiedliche Straßenverhältnisse - Übungen 1 - Anhalteweg - Übungen 2 - Allgemeine quadratische Funktion - Übungen 3
Aufgabe 1: Anhalteweg Die Funktion s(v) = 0,1v2 + 1,5v ist ein Beispiel für eine Funktion, die den Zusammenhang zwischen der anfänglichen Geschwindigkeit eines Fahrzeuges in m/s und dem Anhalteweg für einen konkreten Bremsvorgang angibt.
|
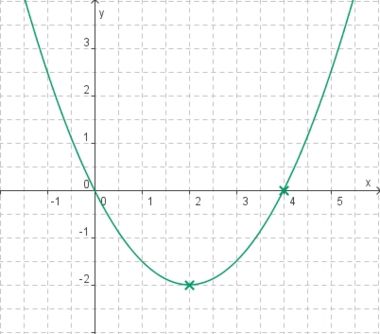
Aufgabe 2: Bestimme a und b
|
Aufgabe 3: Term und Graph zuordnen
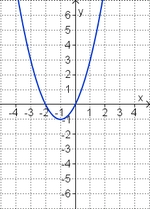
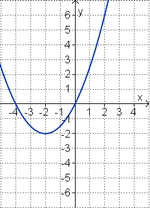
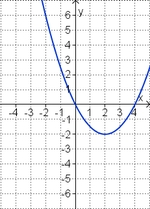
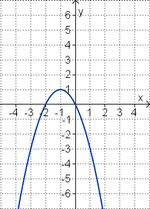
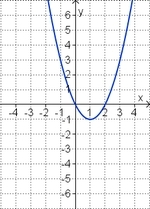
Ordne den Funktionsgraphen den richtigen Term zu.
f(x) = 2x2 - 4x (!Die Parabel ist nach unten geöffnet.) (Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt [-1|6] liegt auf dem Graphen.) (!Der Punkt [-1|-2] liegt auf dem Graphen.) f(x) = - 0,25x2 + 3x (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (!Die Parabel ist enger als die Normalparabel.) (Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|5] liegt auf dem Graphen.) (!Der Punkt [2|7] liegt auf dem Graphen.) Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der y-Achse symmetrisch zueinander sind? (!7x2 und -7x2) (7x2 - 2x und 7x2 + 2x) (!7x2 - 2x und -7x2 + 2x) (!7x2 - 2 und 7x2 + 2) (-7x2 + 2x und -7x2 - 2x) (!7x2 - 2 und 7x2 + 2x) |

|
Als nächstes lernst du die allgemeine quadratische Funktion kennen. |
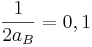 <=>
<=> 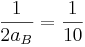 <=> 2aB = 10 <=> aB = 5 (m/s2)
<=> 2aB = 10 <=> aB = 5 (m/s2)