Radioaktiver Zerfall: Unterschied zwischen den Versionen
| Zeile 2: | Zeile 2: | ||
[[Datei:Chernobylreactor 1.jpg|miniatur|x150px|AKW Tschernobyl, Ukraine, 2006; Quelle: http://de.wikipedia.org]] | [[Datei:Chernobylreactor 1.jpg|miniatur|x150px|AKW Tschernobyl, Ukraine, 2006; Quelle: http://de.wikipedia.org]] | ||
| − | Durch die | + | Durch die schrecklichen Ereignisse in Japan vom März 2011, ist es angebracht sich mit dem Abbau von radioaktiven Materialien zu befassen. In allen Schulen Österreichs muss (von den Eltern) angegeben werden, ob den Schülerinnen und Schülern Kaliumjodidtabletten verabreicht werden dürfen, siehe [http://de.wikipedia.org/wiki/Kaliumjodid Kaliumjodid als Strahlenschutz]. In diesem Kapitel erfährst Du mehr über den Abbau von radioaktiven Materialien und den mathematischen Hintergrund der Berechnung von [http://de.wikipedia.org/wiki/Halbwertszeit Halbwertszeiten]. |
| − | Der radioaktive Zerfall wird durch die Gleichung <math>N(t)=a\cdot e^{-b\cdot t}</math> beschrieben, die | + | Der radioaktive Zerfall wird durch die Gleichung <math>N(t)=a\cdot e^{-b\cdot t}</math> beschrieben, die die analytische Lösung einer Differentialgleichung darstellt. Die entsprechende Differenzengleichung sieht so aus: <math>N_{t+1}=N_{t}\cdot e^{b\cdot \tau}</math>, <math>\tau</math> ist der Zeitschritt . |
Bei dem hier gezeigten Beispiel zerfällt ein radioaktives Element in ein zweites stabiles Element. Physikalische Informationen findet man beim [http://www.mineralienatlas.de/lexikon/index.php/Radioaktivit%E4t Mineralienatlas]. | Bei dem hier gezeigten Beispiel zerfällt ein radioaktives Element in ein zweites stabiles Element. Physikalische Informationen findet man beim [http://www.mineralienatlas.de/lexikon/index.php/Radioaktivit%E4t Mineralienatlas]. | ||
| Zeile 10: | Zeile 10: | ||
In der [[:Bild:Bsp_einfacher_zerfall.xls| <b>Lösung mit Tabellenkalkulation</b>]] (xls-Datei, 147 kb) zum radioaktiven Zerfall] ist die Differenzengleichung für ein zerfallendes Element berechnet und die Ergebnisse als Graph dargestellt. Anfangskernanzahl, Zerfallsparameter und Zeitschritt können variert werden. | In der [[:Bild:Bsp_einfacher_zerfall.xls| <b>Lösung mit Tabellenkalkulation</b>]] (xls-Datei, 147 kb) zum radioaktiven Zerfall] ist die Differenzengleichung für ein zerfallendes Element berechnet und die Ergebnisse als Graph dargestellt. Anfangskernanzahl, Zerfallsparameter und Zeitschritt können variert werden. | ||
| − | + | Beispiel zum Radioaktiven Zerfall stehen unter [[Diskret_-_kontinuierlich#Beispiele_zum_radioaktiven_Zerfall|<b>hier</b>]] für dich bereit. | |
| − | Die Herleitung der analytischen Lösung | + | Die Herleitung der analytischen Lösung mit allen Rechenschritten findest Du unter [[Diskret_-_kontinuierlich#Radioaktiver_Zerfall_-_analytische_Herleitung|<b>hier</b>]]. |
| − | [[ | + | [[Diskret - kontinuierlich|Zurück zum Lernpfad]] |
Version vom 11. August 2011, 13:43 Uhr
Durch die schrecklichen Ereignisse in Japan vom März 2011, ist es angebracht sich mit dem Abbau von radioaktiven Materialien zu befassen. In allen Schulen Österreichs muss (von den Eltern) angegeben werden, ob den Schülerinnen und Schülern Kaliumjodidtabletten verabreicht werden dürfen, siehe Kaliumjodid als Strahlenschutz. In diesem Kapitel erfährst Du mehr über den Abbau von radioaktiven Materialien und den mathematischen Hintergrund der Berechnung von Halbwertszeiten.
Der radioaktive Zerfall wird durch die Gleichung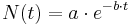 
beschrieben, die die analytische Lösung einer Differentialgleichung darstellt. Die entsprechende Differenzengleichung sieht so aus: 
, 
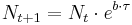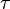ist der Zeitschritt .
Bei dem hier gezeigten Beispiel zerfällt ein radioaktives Element in ein zweites stabiles Element. Physikalische Informationen findet man beim Mineralienatlas.
In der Lösung mit Tabellenkalkulation (xls-Datei, 147 kb) zum radioaktiven Zerfall] ist die Differenzengleichung für ein zerfallendes Element berechnet und die Ergebnisse als Graph dargestellt. Anfangskernanzahl, Zerfallsparameter und Zeitschritt können variert werden.
Beispiel zum Radioaktiven Zerfall stehen unter hier für dich bereit.
Die Herleitung der analytischen Lösung mit allen Rechenschritten findest Du unter hier.
