Quadratische Funktionen - Bremsweg: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | ||
[[Einführung_in_quadratische_Funktionen|Einführung]] - [[Quadratische_Funktionen_-_Bremsweg|Bremsweg]] - [[Quadratische_Funktionen_-_Bremsbeschleunigung|Unterschiedliche Straßenverhältnisse]] - [[Quadratische_Funktionen_-_Übungen|Übungen]] - [[Quadratische_Funktionen_-_Anhalteweg|Anhalteweg]] | [[Einführung_in_quadratische_Funktionen|Einführung]] - [[Quadratische_Funktionen_-_Bremsweg|Bremsweg]] - [[Quadratische_Funktionen_-_Bremsbeschleunigung|Unterschiedliche Straßenverhältnisse]] - [[Quadratische_Funktionen_-_Übungen|Übungen]] - [[Quadratische_Funktionen_-_Anhalteweg|Anhalteweg]] | ||
| + | - [[Quadratische_Funktionen_-_Teste_dein_Wissen|Teste dein Wissen!]] | ||
</div> | </div> | ||
Version vom 11. Oktober 2008, 23:19 Uhr
Einführung - Bremsweg - Unterschiedliche Straßenverhältnisse - Übungen - Anhalteweg - Teste dein Wissen!
Einstieg
Die Frage nach dem Bremsweg ist gar nicht mal so einfach. Zunächst wird man wohl annehmen, dass ein Auto bei doppelter Geschwindigkeit auch einen doppelt so langen Bremsweg hat. Diese Frage wurde am 6. April 2008 bei kopfball.de untersucht:
Ist bei doppelter Geschwindigkeit auch der Bremsweg doppelt so lang?
Tabelle, Graph und Formel
Die Polizei hat Messungen durchgeführt, um den Zusammenhang zwischen der Geschwindigkeit eines Autos und seinem Bremsweg zu erkunden. Klar ist: Je schneller eine Auto fährt, desto länger ist sein Bremsweg. Aber ist das wirklich so einfach...?
Du kannst den Zusammenhang selbst untersuchen. Hier sind die Daten, die die Polizei gesammelt hat:
| Geschwindigkeit (in km/h) | 10 | 20 | 30 | 40 | 50 | 80 | 100 | 120 |
| Bremsweg (in m) | 1 | 4 | 9 | 16 | 25 | 64 | 100 | 144 |
|
a) Stelle die Daten aus der Tabelle in einem Koordinatensystem dar. Trage dabei nach rechts die Geschwindigkeit (in km/h) und nach oben den Bremsweg (in m) an. b) Verbinde die Punkte zu einem Funktionsgraphen (der keine "Ecken" haben sollte). c) Ermittle anhand des Graphen einen Schätzwert für den Bremsweg bei 70 km/h. |
- Lösung:
|
a) Zwischen den Daten der Wertetabelle besteht ein ganz bestimmter Zusammenhang. Versuche eine Formel zu finden, mit deren Hilfe man aus der Geschwindigkeit den Bremsweg berechnen kann. b) In der Fahrschule lernt man: BW = v/10 mal v/10 (Bremsweg = Geschwindigkeit durch 10 mal Geschwindigkeit durch 10).
zu a): z.B. Fahrschulformel:
|
Bild ergänzen: Ball, Mädchen, Hr.Mütze
|
a) Entscheide, ob sich Herr Mütze an die Geschwindigkeitsbegrenzung gehalten hatte.
zu a): Nach obiger Tabelle hätte Herr Mütze, falls er sich an die Geschwindigkeitsbegrenzung gehalten hätte, allenfalls einen Bremsweg von 25 m haben dürfen. zu b):
Nach der Formel aus Aufgabe 1 war Herr Mütze 55 km/h schnell.
|

|
Als nächstes erfährst du, wie die Länge des Bremsweges von der "Bremsbeschleunigung" abhängig ist. |
|
Dieser Lernpfad wurde erstellt von:
Reinhard Schmidt, Christian Schmidt, Maria Eirich, Andrea Schellmann und Gabi Jauck |
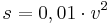 oder
oder 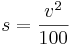 (dabei ist s der Bremsweg in Metern und v die Geschwindigkeit in km/h)
(dabei ist s der Bremsweg in Metern und v die Geschwindigkeit in km/h)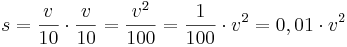 . Die Formeln stimmen also überein.
. Die Formeln stimmen also überein.