Quadratische Funktionen - allgemeine quadratische Funktion: Unterschied zwischen den Versionen

Aus Medienvielfalt-Wiki
Wechseln zu: Navigation, Suche
(layout)
K (hat „Quadratische Funktionen/ Allgemeine quadratische Funktion“ nach „Quadratische Funktionen - allgemeine quadratische Funktion“ verschoben und dabei eine Weiterleitung überschrieben: zurück verschieben)
 
(20 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
−
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;">
+
{{Quadratische Funktionen}}
−
[[Einführung_in_quadratische_Funktionen|Einführung]] - [[Quadratische_Funktionen_-_Bremsweg|Bremsweg]] - [[Quadratische_Funktionen_-_Bremsbeschleunigung|Unterschiedliche Straßenverhältnisse]] - [[Quadratische_Funktionen_-_Übungen1|Übungen (1)]] - [[Quadratische_Funktionen_-_Anhalteweg|Anhalteweg]] - [[Quadratische_Funktionen_-_Übungen2|Übungen (2)]] - [[Quadratische_Funktionen_-_allgemeine quadratische Funktion|Die allgemeine quadratische Funktion]] - [[Quadratische_Funktionen_-_Abschlusstest|Abschlusstest]]
+
 
−
</div>
+
  
 
{|border="0" cellspacing="0" cellpadding="4"
 
{|border="0" cellspacing="0" cellpadding="4"
Zeile 8: Zeile 7:
 
|valign="top"; width=700px|
 
|valign="top"; width=700px|
 
Im vorigen Kapitel hatten wir es mit einer Funktion zu tun, die neben dem reinquadratischen Teil (dem Bremsweg) auch noch einen linearen Teil (den Reaktionsweg) besaß.
 
Im vorigen Kapitel hatten wir es mit einer Funktion zu tun, die neben dem reinquadratischen Teil (dem Bremsweg) auch noch einen linearen Teil (den Reaktionsweg) besaß.
−
Den allgemeinsten Fall einer quadratischen Funktion haben wir, wenn die Funktionsgleichung folgende Form hat: <big>f(x)=ax<sup>2</sup>+bx+c </big>
+
Den allgemeinsten Fall einer quadratischen Funktion haben wir, wenn die Funktionsgleichung folgende Form hat:  
 +
 
 +
<center><big>'''f(x)=ax<sup>2</sup>+bx+c'''</big></center> 
 +
 
  
−
An Funktionen mit derartigen Gleichungen sollst du nun dein Wissen erproben:
 
 
|}
 
|}
  
Zeile 20: Zeile 21:
 
Experimentiere mit dem Applet und erläutere, welchen Einfluss die Parameter a, b und c auf den Verlauf des Graphen haben.
 
Experimentiere mit dem Applet und erläutere, welchen Einfluss die Parameter a, b und c auf den Verlauf des Graphen haben.
  
 +
:{{Lösung versteckt|1=
 +
#<span style="color: red">a bestimmt die Weite und die Öffnung nach oben und unten</span><br />
 +
#<span style="color: blue">b verschiebt den Scheitel</span><br />
 +
#<span style="color: green">c verschiebt den Scheitel für '''c > 0 nach oben''' und für '''c < 0 nach unten'''</span><br />
 +
}}
 
}}
 
}}
  
Zeile 28: Zeile 34:
  
 
{|border="0" cellspacing="0" cellpadding="4"
 
{|border="0" cellspacing="0" cellpadding="4"
−
|align = "left" width="150"|
+
|align = "left" width="200"|
 
{{Arbeiten|  
 
{{Arbeiten|  
 
NUMMER=2|
 
NUMMER=2|
Zeile 38: Zeile 44:
  
 
Graphen liegt.
 
Graphen liegt.
 +
 +
:{{Lösung versteckt|1=
 +
#<span style="color: blue">a = 0,5; b = 2,4; c = - 1</span><br />
 +
#<span style="color: red">a = - 1; b = -3; c = 2</span><br />
 +
#<span style="color: green">a = 0,5; b = - 2,4; c = - 1</span><br />
 +
}}
 +
 
}}
 
}}
  
 
|width=20px|
 
|width=20px|
 
|valign="top"|
 
|valign="top"|
−
<ggb_applet height="500" width="650" filename="Parabeln.ggb" />
+
<ggb_applet height="500" width="650" filename="Quadratisch_allgemein2.ggb" />
 
|}
 
|}
  
Zeile 51: Zeile 64:
 
NUMMER=3|
 
NUMMER=3|
 
ARBEIT=
 
ARBEIT=
−
#Gibt es einen Zusammenhang zwischen dem blauen und grünen Graphen? Experimentiere erneut mit dem ersten Applet und bestätige deine Vermutung.
+
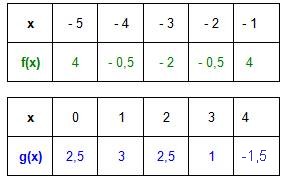
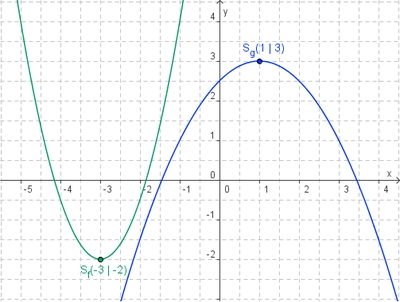
Untersuche nun die Funktionen f mit '''f(x) = 1,5x<sup>2</sup> + 9x + 11,5''' und g mit '''g(x) = 0,5x<sup>2</sup> + x + 2,5'''
−
#Setzt den Satz fort: "Wenn zwei Graphen spiegelbildlich bezüglich der y-Achse liegen, dann ...  
+
#Zeichne mit Hilfe einer Wertetabelle die Graphen G<sub>f</sub> und G<sub>g</sub> in ein gemeinsames Koordinatensystem.  
 +
#Gib die Koordinaten der beiden Scheitel S<sub>f</sub> und S<sub>g</sub> an.
 +
#Vergleiche die beiden Parabeln mit der Normalparabel.
 +
 +
:{{Lösung versteckt|1=
 +
#[[Bild:Quadratisch_Wertetabelle.jpg]] [[Bild:Quadratisch_allgemein3.jpg]]
 +
#<span style="color: green">Scheitel von f: '''S(-3/-2)'''</span>;  <span style="color: blue">Scheitel von g:''' S(1/3)'''</span>
 +
#'''Parabel von f''': Enger als Normalparabel, nach oben geöffnet, verschoben
 +
::'''Parabel von g''': Weiter als Normalparabel, nach unten geöffnet, verschoben
 
}}
 
}}
 +
}}
 +
|}
 +
=== Die allgemeine quadratische Funktion in der Anwendung ===
  
 +
Der Term einer allgemeinen quadratischen Funktion enthält einen reinquadratischen Teil ('''ax<sup>2</sup>'''), einen linearen Teil ('''bx''') und einen konstanten Teil ('''c''').
 +
 +
Du hast in den vorangegangenen Kapiteln erfahren, dass sich beim Bremsen eines Pkws der Zusammenhang zwischen der Geschwindigkeit und dem zurückgelegten Weg durch eine quadratische Funktion der Form '''f(x) = ax<sup>2</sup> + bx''' beschreiben lässt, wobei der reinquadratische Teil den Bremsweg und der lineare Teil den Reaktionsweg bestimmt.<br>
 +
 +
{|border="0" cellspacing="0" cellpadding="4"
 +
|align = "left" width="930"|
 +
{{Arbeiten|
 +
NUMMER=4|
 +
ARBEIT=
 +
Welche Bedeutung hat der konstante Teil des Funktionsterms im Anwendungsbeispiel "Abbremsen eines Pkw"?
 +
 +
:{{Lösung versteckt|1=
 +
 +
:Der lineare Teil gibt den Weg an, den das Fahrzeug zurücklegt, bevor die Gefahrensituation eintritt.
 +
 +
:Beispiel:
 +
::Ein Fahrzeug biegt in eine Straße ein. Nach 30 m sieht der Fahrer, dass vor ihm ein Ball auf die Straße rollt und bremst. Wieviel Meter von der Kreuzung entfernt kommt das Fahrzeug zum Stehen?
 +
 +
::Entfernung zur Kreuzung: s = a·v<sup>2</sup> + b·v + c  mit c = 30m
 +
 +
}}
 +
}}
 
|}
 
|}
  
Zeile 64: Zeile 110:
 
{|border="0" cellspacing="0" cellpadding="4"
 
{|border="0" cellspacing="0" cellpadding="4"
 
|align = "left" width="120"|[[Bild:Maehnrot.jpg|100px]]
 
|align = "left" width="120"|[[Bild:Maehnrot.jpg|100px]]
−
|align = "left"|'''Zum Abschluss: ein Test!'''<br />
+
|align = "left"|
−
[[Bild:Pfeil.gif]] &nbsp; [[Quadratische_Funktionen_-_Abschlusstest|'''Hier geht es weiter''']]'''.'''
+
[[Bild:Pfeil.gif]] &nbsp; [[Quadratische Funktionen - Übungen3|'''Hier geht es weiter''']]'''.'''
  
 
|}
 
|}
 
== Arbeitsblätter ==
 
== Arbeitsblätter ==
 
*[http://www.sinus.lernnetz.de/aufgaben1/materialien/mathematik/sek_I/quadratische_funktionen.doc Arbeitsblatt aus dem Sinus-Lernnetz]
 
*[http://www.sinus.lernnetz.de/aufgaben1/materialien/mathematik/sek_I/quadratische_funktionen.doc Arbeitsblatt aus dem Sinus-Lernnetz]

Aktuelle Version vom 4. Januar 2011, 12:41 Uhr

Einführung - Bremsweg - Unterschiedliche Straßenverhältnisse - Übungen 1 - Anhalteweg - Übungen 2 - Allgemeine quadratische Funktion - Übungen 3


Im vorigen Kapitel hatten wir es mit einer Funktion zu tun, die neben dem reinquadratischen Teil (dem Bremsweg) auch noch einen linearen Teil (den Reaktionsweg) besaß. Den allgemeinsten Fall einer quadratischen Funktion haben wir, wenn die Funktionsgleichung folgende Form hat:

f(x)=ax2+bx+c


  Aufgabe 1  Stift.gif

Experimentiere mit dem Applet und erläutere, welchen Einfluss die Parameter a, b und c auf den Verlauf des Graphen haben.

  1. a bestimmt die Weite und die Öffnung nach oben und unten
  2. b verschiebt den Scheitel
  3. c verschiebt den Scheitel für c > 0 nach oben und für c < 0 nach unten

  Aufgabe 2  Stift.gif

Stelle die drei Schieberegler so ein, dass der schwarze Graph genau auf dem

  1. roten
  2. grünen
  3. blauen

Graphen liegt.

  1. a = 0,5; b = 2,4; c = - 1
  2. a = - 1; b = -3; c = 2
  3. a = 0,5; b = - 2,4; c = - 1


  Aufgabe 3  Stift.gif

Untersuche nun die Funktionen f mit f(x) = 1,5x2 + 9x + 11,5 und g mit g(x) = 0,5x2 + x + 2,5

  1. Zeichne mit Hilfe einer Wertetabelle die Graphen Gf und Gg in ein gemeinsames Koordinatensystem.
  2. Gib die Koordinaten der beiden Scheitel Sf und Sg an.
  3. Vergleiche die beiden Parabeln mit der Normalparabel.
  1. Quadratisch Wertetabelle.jpg Quadratisch allgemein3.jpg
  2. Scheitel von f: S(-3/-2); Scheitel von g: S(1/3)
  3. Parabel von f: Enger als Normalparabel, nach oben geöffnet, verschoben
Parabel von g: Weiter als Normalparabel, nach unten geöffnet, verschoben

Die allgemeine quadratische Funktion in der Anwendung

Der Term einer allgemeinen quadratischen Funktion enthält einen reinquadratischen Teil (ax2), einen linearen Teil (bx) und einen konstanten Teil (c).

Du hast in den vorangegangenen Kapiteln erfahren, dass sich beim Bremsen eines Pkws der Zusammenhang zwischen der Geschwindigkeit und dem zurückgelegten Weg durch eine quadratische Funktion der Form f(x) = ax2 + bx beschreiben lässt, wobei der reinquadratische Teil den Bremsweg und der lineare Teil den Reaktionsweg bestimmt.

  Aufgabe 4  Stift.gif

Welche Bedeutung hat der konstante Teil des Funktionsterms im Anwendungsbeispiel "Abbremsen eines Pkw"?

Der lineare Teil gibt den Weg an, den das Fahrzeug zurücklegt, bevor die Gefahrensituation eintritt.
Beispiel:
Ein Fahrzeug biegt in eine Straße ein. Nach 30 m sieht der Fahrer, dass vor ihm ein Ball auf die Straße rollt und bremst. Wieviel Meter von der Kreuzung entfernt kommt das Fahrzeug zum Stehen?
Entfernung zur Kreuzung: s = a·v2 + b·v + c mit c = 30m



Maehnrot.jpg

Pfeil.gif   Hier geht es weiter.

Arbeitsblätter

Von „http://medienvielfalt.zum.de/index.php?title=Quadratische_Funktionen_-_allgemeine_quadratische_Funktion&oldid=4484“