Wie lange dauern Projekte? - Die Dreiecksverteilung: Unterschied zwischen den Versionen

Aus Medienvielfalt-Wiki
Wechseln zu: Navigation, Suche
 
(20 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
'''[[Benutzer:Peter Hofbauer|Peter Hofbauer]], [[Benutzer:Heidi Metzger-Schuhäker|Heidi Metzger-Schuhäker]], Gabi Bleier'''
 +
 
{{Kasten1000|
 
{{Kasten1000|
  
Zeile 50: Zeile 52:
  
 
{{Arbeiten|NUMMER=|
 
{{Arbeiten|NUMMER=|
−
ARBEIT=Vergleiche das Modell mit den Modellen der diskreten Wahrscheinlichkeitsvereilungen. Welcher grundlegende Unterschied fällt dir auf?
+
ARBEIT=Vergleiche das Modell mit den Modellen der diskreten Wahrscheinlichkeitsvereilungen! Welcher grundlegende Unterschied fällt dir auf?
 
}}
 
}}
  
 
''' Lösung'''
 
''' Lösung'''
−
{{versteckt|Im Gegensatz zu den diskreten Verteilungen kann die Zufallsvariable (in unserem Beispiel die Projektdauer) - zumindest theoretisch - jeden beliebigen Wert annehmen. So kann das Projekt z. B nicht nur 8 oder 9 Tage dauern, sondern auch 8,3 Tage.}}
+
{{versteckt|Im Gegensatz zu den diskreten Verteilungen, kann die Zufallsvariable (in unserem Beispiel die Projektdauer) - zumindest theoretisch - jeden beliebigen Wert annehmen. So kann das Projekt z. B nicht nur 8 oder 9 Tage dauern, sondern auch 8,3 Tage.}}
  
  
Zeile 62: Zeile 64:
  
 
{{Arbeiten|NUMMER=|
 
{{Arbeiten|NUMMER=|
−
ARBEIT= Finde selbst Beispiele für diskrete und kontinuierliche Zufallsvariable.
+
ARBEIT= Finde selbst Beispiele für diskrete und kontinuierliche Zufallsvariable!
 
}}
 
}}
  
Zeile 68: Zeile 70:
 
'''weiter im Modell'''
 
'''weiter im Modell'''
 
{{Arbeiten|NUMMER=|
 
{{Arbeiten|NUMMER=|
−
ARBEIT=Wie sieht die grafische Umsetzung des Wahrscheinlichkeitsmodells aus? Skizziere den Verlauf der Wahrscheinlichkeitsfunktion.
+
ARBEIT=Wie sieht die grafische Umsetzung des Wahrscheinlichkeitsmodells aus? Skizziere den Verlauf der Wahrscheinlichkeitsfunktion!
 
}}
 
}}
  
Zeile 82: Zeile 84:
  
  
−
<pre>Vielleicht sind beim Zeichnen der Skizze schon ein paar Fragen aufgetaucht, die man noch genauer klären muss:
+
Vielleicht sind beim Zeichnen der Skizze schon ein paar Fragen aufge-
−
 
+
taucht, die man noch genauer klären muss:
−
* Wie sieht die Wahrscheinlichkeit für eine Projektdauer vor dem 0. Tag bzw. nach dem 14. Tag aus?
+
- Wie sieht die Wahrscheinlichkeit für eine Projektdauer vor
−
und
+
  dem 0. Tag bzw. nach dem 14. Tag aus?
−
* Wie laesst sich diese interpretieren?</pre>
+
und
 +
- Wie laesst sich diese interpretieren?
  
 
'''Antwort:'''
 
'''Antwort:'''
Zeile 94: Zeile 97:
  
  
−
<pre>Die Dichtefunktion soll bei X=10 ihr Maximum haben.
+
Die Dichtefunktion soll bei X=10 ihr Maximum haben.
−
Welchen Funktionswert nimmt sie an dieser Stelle an?
+
Welchen Funktionswert nimmt sie an dieser Stelle an?
−
Ist er beliebig oder gibt es einen einzig möglichen Wert für die konkrete Aufgabenstellung?</pre>
+
Ist er beliebig oder gibt es einen einzig möglichen Wert für die
 +
konkrete Aufgabenstellung?
  
 
Dazu müssen wir uns erst einmal überlegen, wie man aus einer Dichtefunktion Wahrscheinlichkeiten ablesen kann.<br />
 
Dazu müssen wir uns erst einmal überlegen, wie man aus einer Dichtefunktion Wahrscheinlichkeiten ablesen kann.<br />
−
Im diskreten Fall war es einfach, die Wahrscheinlichkeit für das Eintreten eines Ereignisses in einem bestimmten Intervall zu bestimmen - werden die Einzelwahrscheinlichkeiten aller Ereignisse addiert, die sich im gesuchten Intervall befinden, so erhält man die gesuchte Wahrscheinlichkeit.<br />
+
Im diskreten Fall war es einfach, die Wahrscheinlichkeit für das Eintreten eines Ereignisses in einem bestimmten Intervall zu bestimmen: Addiert man die Einzelwahrscheinlichkeiten aller Ereignisse im gegebenen Intervall, so erhält man die gesuchte Gesamtwahrscheinlichkeit.<br />
 
Aber wie geht man im kontinuierlichen Fall vor?
 
Aber wie geht man im kontinuierlichen Fall vor?
 
Im kontinuierlichen Fall gibt es in jedem Intervall unendlich viele Werte, die die Zufallsvariable annehmen kann. Das Aufsummieren wie im diskreten Fall schlägt damit also fehl. Du hast allerdings die mathematische Idee des Übergangs von diskret zu kontinuierlich bereits kennen gelernt.
 
Im kontinuierlichen Fall gibt es in jedem Intervall unendlich viele Werte, die die Zufallsvariable annehmen kann. Das Aufsummieren wie im diskreten Fall schlägt damit also fehl. Du hast allerdings die mathematische Idee des Übergangs von diskret zu kontinuierlich bereits kennen gelernt.
Zeile 117: Zeile 121:
  
 
Als Wiederholung zum Thema Integralrechnung siehe gegebenenfalls die Seiten von [http://mathe-online.at/ressourcen/?s=int mathe-online]
 
Als Wiederholung zum Thema Integralrechnung siehe gegebenenfalls die Seiten von [http://mathe-online.at/ressourcen/?s=int mathe-online]
−
 
  
 
== Wir präzisieren die Fragestellung==
 
== Wir präzisieren die Fragestellung==
−
Um einmal eine konkrete Aufgabenstellung lösen zu können stellen wir uns die Frage, wie groß die Wahrscheinlichkeit ist, dass das Projekt 7 bis 9 Tage dauert.
+
Um einmal eine konkrete Aufgabenstellung lösen zu können, stellen wir uns die Frage, wie groß die Wahrscheinlichkeit ist, dass das Projekt 7 bis 9 Tage dauert.
  
−
Um die Frage beantworten zu können, müssen wir - ausgehend von der zuvor bereits erstellen Skizze - die Dichtefunktion auch mathematisch beschreiben können.
+
Um die Frage beantworten zu können, müssen wir - ausgehend von der zuvor bereits erstellten Skizze - die Dichtefunktion auch mathematisch beschreiben können.
 
Vieles wissen wir bereits über diese Funktion, ein Detail fehlt uns aber noch: der Funktionswert für den 10. Tag, an dem das Projekt mit größter Wahrscheinlichkeit beendet wird.
 
Vieles wissen wir bereits über diese Funktion, ein Detail fehlt uns aber noch: der Funktionswert für den 10. Tag, an dem das Projekt mit größter Wahrscheinlichkeit beendet wird.
 
In diesem Zusammenhang solltest du folgende Frage beantworten:
 
In diesem Zusammenhang solltest du folgende Frage beantworten:
Zeile 143: Zeile 146:
 
<ggb_applet height="400" width="800" filename="DreieckHoehe.ggb" />
 
<ggb_applet height="400" width="800" filename="DreieckHoehe.ggb" />
 
}}
 
}}
−
 
  
 
== Geschafft ==
 
== Geschafft ==
Zeile 149: Zeile 151:
 
<br /><br />
 
<br /><br />
 
{{Arbeiten|NUMMER=|
 
{{Arbeiten|NUMMER=|
−
ARBEIT=Das Berechnen der Fläche unter der Dichtefunktion im Intervall [7;9] sollte für dich keine Schwierigkeiten bereiten.<br />
+
ARBEIT=Das Berechnen der Fläche unter der Dichtefunktion im Intervall [7;9] sollte dir keine Schwierigkeiten bereiten.<br />
 
''Wenn doch, dann überlege am besten zuerst, welche geometrische Form die gesuchte Fläche besitzt.''}}
 
''Wenn doch, dann überlege am besten zuerst, welche geometrische Form die gesuchte Fläche besitzt.''}}
  
Zeile 168: Zeile 170:
 
Allgemein nennt man eine Verteilung, welche durch das von uns gewählte Modell entsteht, eine ''Dreiecksverteilung'' (warum wohl)?
 
Allgemein nennt man eine Verteilung, welche durch das von uns gewählte Modell entsteht, eine ''Dreiecksverteilung'' (warum wohl)?
  
−
Die Verallgemeinerung unseres Verteilungsmodells setzt den Startpunkt nicht an die Stelle 0, sondern ganz allgemein an eine Stelle a (=optimistischster Wert, minimaler Wert), den Endpunkt an die Stelle b (=pessimistischster Wert, maximaler Wert) und den Fußpunkt des Dreiecks an eine beliebige Stelle c im Intervall [a;b] (=vermutlicher Wert, wahrscheinlichster Wert).
+
Die Verallgemeinerung unseres Verteilungsmodells setzt den Startpunkt nicht an die Stelle 0, sondern ganz allgemein an eine Stelle a (= optimistischster Wert, minimaler Wert), den Endpunkt an die Stelle b (= pessimistischster Wert, maximaler Wert) und den Fußpunkt des Dreiecks an eine beliebige Stelle c im Intervall [a ; b] (= vermutlicher Wert, wahrscheinlichster Wert).
 
<br /><br />
 
<br /><br />
 
{{Arbeiten|NUMMER=|
 
{{Arbeiten|NUMMER=|
−
ARBEIT=Versuche selbst, die Dichtefunktion der Dreiecksverteilung zu definieren.
+
ARBEIT=Versuche selbst, die Dichtefunktion der Dreiecksverteilung zu definieren!
  
−
''Ein Tipp:'' Modelliere zuerst die Funktion im Bereich [a,c] und dann im Bereich [c,b] und fasse diese beiden Ergebnisse zu einer stückweise definierten Funktion zusammen. Die Lösung führt über die Bestimmung des Funktionswertes an der Stelle c (=der Höhe des Dreiecks). Die nachfolgende Grafik soll dir bei deinen Überlegungen behilflich sein.
+
''Ein Tipp:'' Modelliere zuerst die Funktion im Bereich [a ; c] und dann im Bereich [c ; b] und fasse diese beiden Ergebnisse zu einer stückweise definierten Funktion zusammen! Die Lösung führt über die Bestimmung des Funktionswertes an der Stelle c (= der Höhe des Dreiecks). Die nachfolgende Grafik soll dir bei deinen Überlegungen behilflich sein.
 
<br />
 
<br />
 
[[Bild:BildDreieck.png|thumb|center|250px|Dichtefunktion einer Dreiecksverteilung]]
 
[[Bild:BildDreieck.png|thumb|center|250px|Dichtefunktion einer Dreiecksverteilung]]
Zeile 185: Zeile 187:
 
<br />
 
<br />
  
−
um ganz exakt zu sein sollte man die Dichtefunktion auch noch für die Intervalle [-inf,a] und [b, inf] definieren. In diesen Bereichen ist die Funktion immer 0 und<br />somit erhält man letztendlich für die Dreiecksverteilung die Dichtefunktion
+
Um ganz exakt zu sein sollte man die Dichtefunktion auch noch für die Intervalle [-inf ; a] und [b ; inf] definieren. In diesen Bereichen ist die Funktion immer 0 und somit erhält man letztendlich für die Dreiecksverteilung die Dichtefunktion:
 
<br />
 
<br />
  
−
{{versteckt|<math>f(x)=\begin{cases} 0 & \mbox{  } \forall x \in  (\infty,a] \\ {{2 \over {(b-a) \cdot (c-a)}}  (x-a)} & \mbox{  } \forall x \in [a,c] \\ {{2 \over {(b-a) \cdot (c-b)}} (x-b)} & \mbox{  } \forall x \in [c,b] \\ 0 & \mbox{  } \forall x \in  [b,\infty)  \end{cases}</math>}}
+
{{versteckt|<math>f(x)=\begin{cases} 0 & \mbox{  } \forall x \in  (\infty,a] \\ {{2 \over {(b-a) \cdot (c-a)}}  (x-a)} & \mbox{  } \forall x \in [a,c] \\ {{2 \over {(b-a) \cdot (c-b)}} (x-b)} & \mbox{  } \forall x \in [c,b] \\ 0 & \mbox{  } \forall x \in  [b,\infty)  \end{cases}</math> <br />}}
−
 
+
<br />
  
−
 
+
= Zum Schluss=
−
= zum Schluss=
+
  
 
{{Arbeiten|NUMMER=|
 
{{Arbeiten|NUMMER=|
Zeile 200: Zeile 201:
  
 
'''Lösung:'''
 
'''Lösung:'''
−
{{versteckt|Die Berechnung der Wahrscheinlichkeit für einen ganz bestimmten Wert (in unserem Beispiel für das Projektende zu einem ganz bestimmten Zeitpunkt) führt auf die Berechnung des Integrals an einer einzigen Stelle. Da das Integral für einen bestimmten Wert aber immer gleich 0 ist macht also die Frage nach ganz bestimmten Ausgängen bei kontinuierlichen Verteilungen keinen Sinn. Nur die Frage nach der Wahrscheinlichkeit für bestimmte Intervalle der Zufallsvariablen lassen sich beantworten.}}
+
{{versteckt|Die Berechnung der Wahrscheinlichkeit für einen ganz bestimmten Wert (in unserem Beispiel für das Projektende zu einem ganz bestimmten Zeitpunkt) führt auf die Berechnung des Integrals an einer einzigen Stelle. Da das Integral für einen bestimmten Wert aber immer gleich 0 ist, macht also die Frage nach ganz bestimmten Ausgängen bei kontinuierlichen Verteilungen keinen Sinn. Nur die Frage nach der Wahrscheinlichkeit für bestimmte Intervalle der Zufallsvariablen lassen sich beantworten.}}
−
 
+
<br />
  
 
= Versuche es selbst=
 
= Versuche es selbst=
−
Das folgende GeoGebra-Applet soll dir bei der Bearbeitung des Arbeitsplatzes helfen.
+
Das folgende GeoGebra-Applet soll dir bei der Bearbeitung des untenstehenden Arbeitsblattes helfen.
 
Versuche die Aufgaben selbstständig zu lösen und nimm das Applet als Unterstützung zuhilfe.
 
Versuche die Aufgaben selbstständig zu lösen und nimm das Applet als Unterstützung zuhilfe.
  
−
<span style="color: red">Wie bettet man das Applet ein???</span>
+
<ggb_applet height="400" width="800" filename="DreieckVerteilung.ggb" />
−
 
+
−
{{pdf|Aufgaben_zur_Dreiecksverteilung.pdf|Anwendungsbeispiele}}
+
  
 +
<br />
 +
<br />
 +
{{pdf|Aufgaben_zur_Dreiecksverteilung.pdf|Anwendungsaufgaben}}
 +
<br /><br />
  
−
== im WWW==
+
= im WWW=
−
<span style="color: red">INTERNETADRESSEN EINFÜGEN</span>
+
[http://www.uni-konstanz.de/FuF/wiwi/heiler/os/vt-drei.html Java-Applet zur Dreiecksverteilung der Uni Konstanz]<br />
 +
[http://pm.hs-augsburg.de/glossar/Dreiecksverteilung Eine Zusammenfassung der Eigenschaften der Dreiecksverteilung von der Hochschule Augsburg]<br />
 +
[http://www.decisionsciences.org/DecisionLine/Vol31/31_3/31_3clas.pdf Ein Artikel zur Umsetzung der Dreiecksverteilung mit MS Excel (von Rick Hesse, Graziadia Graduate School of Business, Pepperdine University)]<br />

Aktuelle Version vom 4. Mai 2009, 14:31 Uhr

Peter Hofbauer, Heidi Metzger-Schuhäker, Gabi Bleier

Nuvola apps edu miscellaneous.png
Über diesen Lernpfad

Dieser Lernpfad bietet eine kurze Einführung in das Thema kontinuierliche Wahrscheinlichkeits- und Verteilungsfunktionen. Die Einführung soll in einem Beispiel erfolgen, bei dem versucht wird, die Dauer von Projekten vorherzusagen.

Kompetenzen:

Das kannst du schon:

  • Integrale als Übergang von diskreten zu kontinuierlichen Modellen verstehen
  • mit diskreten Wahrscheinlichkeits- und Verteilungsfunktionen arbeiten
  • Schieberegler zur Parametervariation verwenden
  • Funktionseigenschaften grafisch interpretieren
  • grafische Darstellungen durch Terme formulieren

Das kannst du lernen:

  • Reale Problemstellungen mithilfe mathematischer Modelle beschreiben und diese exaktifizieren
  • Skizzen und mathematische Vorgaben kombinieren und zu einem mathematischen Modell verbinden
  • die Integralrechnung im Bereich der Wahrscheinlichkeitsrechnung einsetzen
  • Fragestellungen aus dem Bereich der Wahrscheinlichkeit mathematisch formulieren
  • Möglichkeiten und Grenzen der kontinuierlichen Wahrscheinlichkeits- und Verteilungsfunktionen erkennen
  Pfeil.gif Für die Lehrerinnen und Lehrer:

Pdf20.gif Didaktischer Kommentar


Inhaltsverzeichnis

Projekte dauern ... wie lange???

Projekte lassen sich zeitlich oft nicht genau planen: Neue Aufgaben benötigen zur Lösung Zeit - wie viel, das ist zu Projektbeginn oft unklar. Im besten Fall ist die Aufgabenstellung bereits aus früheren Projekten bekannt und somit bereits gelöst. Im schlechtesten Fall erweist sich die Aufgabe als so komplex, dass das Projekt irgendwann abgebrochen und die Suche nach einer Lösung der Aufgabe eingestellt wird. Doch normalerweise lassen sich Projekte innerhalb einer angemessenen Zeit abschließen. Idealerweise hat man aus früheren Projekten schon Erfahrungswerte bezüglich der Projektdauer gesammelt und kann diese somit abschätzen.


Die Ausgangssituation

Ein Konzern stellt uns eine Aufgabe, die in einem Projektteam gelöst werden soll. Für die Lösung hat das Team maximal 14 Tage Zeit. Der Projektleiter war bereits früher mit ähnlichen Projekten betraut und schätzt die voraussichtliche Projektdauer auf 10 Tage.


Die Frage

Lässt sich mithilfe der bekannten Zeitangaben eine Methode entwicklen, die es uns ermöglicht, die tatsächliche Projektdauer vorherzusagen? Oder mathematisch formuliert: Können wir die Wahrscheinlichkeit dafür berechnen, dass das Projekt eine bestimmte Zeit dauern wird?


Das Modell

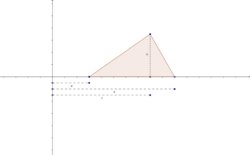
Da der Projektleiter mit einer voraussichtlichen Projektdauer von 10 Tagen rechnet, soll die Wahrscheinlichkeit für die Dauer von 10 Tagen am größten sein. Über die Zeitspanne von 0 bis 10 Tagen bzw. von 10 bis 14 Tagen ist es am einfachsten, eine lineare Zu- bzw. Abnahme der Wahrscheinlichkeit zu modellieren.


  Aufgabe   Stift.gif

Vergleiche das Modell mit den Modellen der diskreten Wahrscheinlichkeitsvereilungen! Welcher grundlegende Unterschied fällt dir auf?


Lösung

Im Gegensatz zu den diskreten Verteilungen, kann die Zufallsvariable (in unserem Beispiel die Projektdauer) - zumindest theoretisch - jeden beliebigen Wert annehmen. So kann das Projekt z. B nicht nur 8 oder 9 Tage dauern, sondern auch 8,3 Tage.


Maehnrot.jpg
Merke:

Eine Zufallsvariable, die (in einem Intervall) jeden beliebigen Wert annehmen kann, nennt man kontinuierliche Zufallsvariable.


  Aufgabe   Stift.gif

Finde selbst Beispiele für diskrete und kontinuierliche Zufallsvariable!


weiter im Modell

  Aufgabe   Stift.gif

Wie sieht die grafische Umsetzung des Wahrscheinlichkeitsmodells aus? Skizziere den Verlauf der Wahrscheinlichkeitsfunktion!


Lösung


Maehnrot.jpg
Merke:

Die Wahrscheinlichkeitsfunktion einer kontinuierlichen Zufallsvariablen nennt man Dichtefunktion. 


Vielleicht sind beim Zeichnen der Skizze schon ein paar Fragen aufge-
taucht, die man noch genauer klären muss:
- Wie sieht die Wahrscheinlichkeit für eine Projektdauer vor
  dem 0. Tag bzw. nach dem 14. Tag aus?
und
- Wie laesst sich diese interpretieren?

Antwort:

Da das Projekt ja kaum beendet sein kann, bevor es begonnen hat, muss die Wahrscheinlichkeit für ein Projektende vor dem 0. Tag natürlich 0 sein.

Ähnliches gilt für ein Projektende nach dem 14. Tag. Da man weiss, dass das Team maximal 14 Tage Zeit hat, ist ein Ende des Projekts zu einem späteren Zeitpunkt ebenfalls unmöglich - daher ist auch hierfür die Wahrscheinlichkeit 0.


Die Dichtefunktion soll bei X=10 ihr Maximum haben.
Welchen Funktionswert nimmt sie an dieser Stelle an?
Ist er beliebig oder gibt es einen einzig möglichen Wert für die
konkrete Aufgabenstellung?

Dazu müssen wir uns erst einmal überlegen, wie man aus einer Dichtefunktion Wahrscheinlichkeiten ablesen kann.
Im diskreten Fall war es einfach, die Wahrscheinlichkeit für das Eintreten eines Ereignisses in einem bestimmten Intervall zu bestimmen: Addiert man die Einzelwahrscheinlichkeiten aller Ereignisse im gegebenen Intervall, so erhält man die gesuchte Gesamtwahrscheinlichkeit.
Aber wie geht man im kontinuierlichen Fall vor? Im kontinuierlichen Fall gibt es in jedem Intervall unendlich viele Werte, die die Zufallsvariable annehmen kann. Das Aufsummieren wie im diskreten Fall schlägt damit also fehl. Du hast allerdings die mathematische Idee des Übergangs von diskret zu kontinuierlich bereits kennen gelernt.


  Aufgabe   Stift.gif

In welchem Zusammenhang hast du schon einmal den Schritt von Summen im diskreten Fall zu "Summen" bei kontinuierlichen Prozessen durchgeführt?


Lösung

Flächenberechnung bei (stetigen) Funktionen: Aus Summen von Rechtecksflächen wurde das Integral.


Maehnrot.jpg
Merke:

Die Wahrscheinlichkeit eines Ereignisses in einem gegebenen Intervall läuft auf die Berechnung der Fläche der Dichtefunktion innerhalb dieses Intervalls hinaus.


Als Wiederholung zum Thema Integralrechnung siehe gegebenenfalls die Seiten von mathe-online

Wir präzisieren die Fragestellung

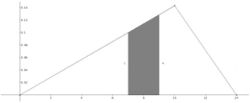
Um einmal eine konkrete Aufgabenstellung lösen zu können, stellen wir uns die Frage, wie groß die Wahrscheinlichkeit ist, dass das Projekt 7 bis 9 Tage dauert.

Um die Frage beantworten zu können, müssen wir - ausgehend von der zuvor bereits erstellten Skizze - die Dichtefunktion auch mathematisch beschreiben können. Vieles wissen wir bereits über diese Funktion, ein Detail fehlt uns aber noch: der Funktionswert für den 10. Tag, an dem das Projekt mit größter Wahrscheinlichkeit beendet wird. In diesem Zusammenhang solltest du folgende Frage beantworten:

  Aufgabe   Stift.gif

Wie groß muss die Gesamtfläche unterhalb der Dichtefunktion (d. h. in diesem Fall die Fläche des Dreiecks) sein?

Lösung:

Die Fläche unterhalb der Dichtefunktion muss 1 sein (irgendein eines aller möglichen Ereignis muss ja eintreten!)

Das bedeutet nun, dass die Höhe des Dreiecks so gewählt werden müssen, dass die Dreiecksfläche genau den Wert 1 ergibt.


  Aufgabe   Stift.gif

Mithilfe der Formel *Dreiecksfläche = halbe Seitenlänge mal zugehöriger Höhe* kannst du selbst das Ergebnis berechnen.


Überprüfe dein Ergebnis anhand der folgenden Simulation!

Geschafft

Somit haben wir UNSER Projekt bereits gelöst.

  Aufgabe   Stift.gif

Das Berechnen der Fläche unter der Dichtefunktion im Intervall [7;9] sollte dir keine Schwierigkeiten bereiten.
Wenn doch, dann überlege am besten zuerst, welche geometrische Form die gesuchte Fläche besitzt.


gesuchte Fläche


Lösung:

z. B. lässt sich mittels Strahlensatz die Länge der beiden parallelen Seiten a und c des Trapezes bestimmen: 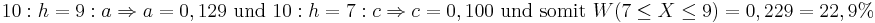{10 : h = 9 : a} \Rightarrow {a = 0,129} \mbox{ und } {10 : h = 7 : c} \Rightarrow c = 0,100 \mbox{ und somit } W(7 \le X \le 9)=0,229 = 22,9%

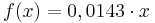oder mittels einer linearen Funktion für den Bereich von 0 bis 10: f(x)=0,0143 \cdot x (warum?) und jetzt mittels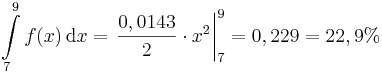 \int\limits_{7}^{9} f(x)\, \mathrm{d}x = \left. {0,0143 \over 2} \cdot x^2 \right \vert ^9_7 = 0,229 = 22,9%


Die Antwort

Die Wahrscheinlichkeit dafür, dass das Projekt nach 7 bis 9 Tagen beendet ist, liegt nach unserem Modell bei ca. 23%.


Dreiecksverteilung

Allgemein nennt man eine Verteilung, welche durch das von uns gewählte Modell entsteht, eine Dreiecksverteilung (warum wohl)?

Die Verallgemeinerung unseres Verteilungsmodells setzt den Startpunkt nicht an die Stelle 0, sondern ganz allgemein an eine Stelle a (= optimistischster Wert, minimaler Wert), den Endpunkt an die Stelle b (= pessimistischster Wert, maximaler Wert) und den Fußpunkt des Dreiecks an eine beliebige Stelle c im Intervall [a ; b] (= vermutlicher Wert, wahrscheinlichster Wert).

  Aufgabe   Stift.gif

Versuche selbst, die Dichtefunktion der Dreiecksverteilung zu definieren!

Ein Tipp: Modelliere zuerst die Funktion im Bereich [a ; c] und dann im Bereich [c ; b] und fasse diese beiden Ergebnisse zu einer stückweise definierten Funktion zusammen! Die Lösung führt über die Bestimmung des Funktionswertes an der Stelle c (= der Höhe des Dreiecks). Die nachfolgende Grafik soll dir bei deinen Überlegungen behilflich sein.

Dichtefunktion einer Dreiecksverteilung


Lösung:

A={{{(b-a)} \cdot h} \over 2} = 1 \Rightarrow h={2 \over {b-a}} \mbox{ und } {f(x)=\begin{cases} {h \over {c-a}} \cdot {(x-a)} & \mbox{ } \forall x \in [a,c] \\ {h \over {c-b}} \cdot {(x-b)} & \mbox{ } \forall x \in [c,b] \end{cases}}
bzw. wenn man das Ergebnis für h einsetzt:

f(x)=\begin{cases} {{2 \over {(b-a) \cdot (c-a)}} (x-a)} & \mbox{ } \forall x \in [a,c] \\ {{2 \over {(b-a) \cdot (c-b)}} (x-b)} & \mbox{ } \forall x \in [c,b] \end{cases}


Um ganz exakt zu sein sollte man die Dichtefunktion auch noch für die Intervalle [-inf ; a] und [b ; inf] definieren. In diesen Bereichen ist die Funktion immer 0 und somit erhält man letztendlich für die Dreiecksverteilung die Dichtefunktion:

f(x)=\begin{cases} 0 & \mbox{ } \forall x \in (\infty,a] \\ {{2 \over {(b-a) \cdot (c-a)}} (x-a)} & \mbox{ } \forall x \in [a,c] \\ {{2 \over {(b-a) \cdot (c-b)}} (x-b)} & \mbox{ } \forall x \in [c,b] \\ 0 & \mbox{ } \forall x \in [b,\infty) \end{cases}


Zum Schluss

  Aufgabe   Stift.gif

Was lässt sich über die Wahrscheinlichkeit für einen ganz bestimmten Wert aussagen (bei der Dreiecksverteilung aber auch ganz allgemein bei kontinuierlichen Verteilungen)?


Lösung:

Die Berechnung der Wahrscheinlichkeit für einen ganz bestimmten Wert (in unserem Beispiel für das Projektende zu einem ganz bestimmten Zeitpunkt) führt auf die Berechnung des Integrals an einer einzigen Stelle. Da das Integral für einen bestimmten Wert aber immer gleich 0 ist, macht also die Frage nach ganz bestimmten Ausgängen bei kontinuierlichen Verteilungen keinen Sinn. Nur die Frage nach der Wahrscheinlichkeit für bestimmte Intervalle der Zufallsvariablen lassen sich beantworten.


Versuche es selbst

Das folgende GeoGebra-Applet soll dir bei der Bearbeitung des untenstehenden Arbeitsblattes helfen. Versuche die Aufgaben selbstständig zu lösen und nimm das Applet als Unterstützung zuhilfe.



Pdf20.gif Anwendungsaufgaben

im WWW

Java-Applet zur Dreiecksverteilung der Uni Konstanz
Eine Zusammenfassung der Eigenschaften der Dreiecksverteilung von der Hochschule Augsburg
Ein Artikel zur Umsetzung der Dreiecksverteilung mit MS Excel (von Rick Hesse, Graziadia Graduate School of Business, Pepperdine University)

Von „http://medienvielfalt.zum.de/index.php?title=Wie_lange_dauern_Projekte%3F_-_Die_Dreiecksverteilung&oldid=3872“