Anwendungen in der Physik: Unterschied zwischen den Versionen
(→Anwendungen in der Physik) |
(Avatare auskommentiert) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 19: | Zeile 19: | ||
}} | }} | ||
</div> | </div> | ||
| + | |||
| + | <br> | ||
{| | {| | ||
| | | | ||
<span style="background-color:yellow;">Hefteintrag:</span> Formuliere eine Überschrift und mache dir Notizen zu den Aufgaben! | <span style="background-color:yellow;">Hefteintrag:</span> Formuliere eine Überschrift und mache dir Notizen zu den Aufgaben! | ||
| + | |||
| + | <br> | ||
| + | |||
| + | ---- | ||
Es gibt viele periodische Vorgänge, also Vorgänge, die sich nach einer bestimmten Zeit wiederholen. Zeichnet man deren zeitlichen Verlauf auf, so erhält man einen sinusförmigen Graphen. | Es gibt viele periodische Vorgänge, also Vorgänge, die sich nach einer bestimmten Zeit wiederholen. Zeichnet man deren zeitlichen Verlauf auf, so erhält man einen sinusförmigen Graphen. | ||
| − | ||{{#ev:youtube|a6KwTw2uM08|150}} | + | ||<!--{{#ev:youtube|a6KwTw2uM08|150}}--> |
|} | |} | ||
| Zeile 38: | Zeile 44: | ||
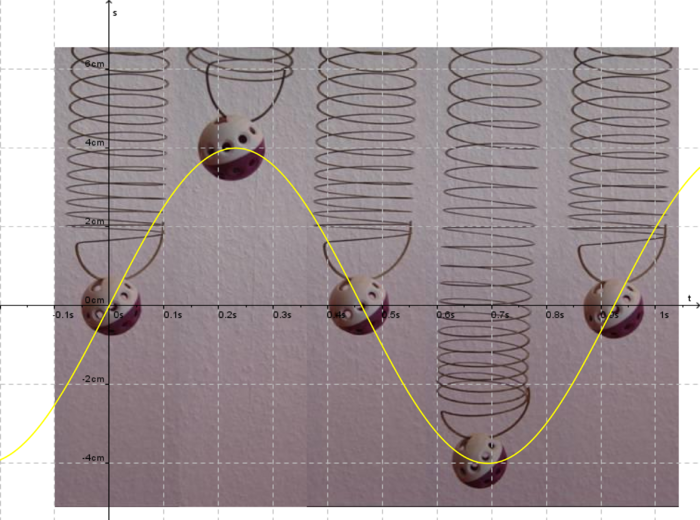
# Gib die zugehörige Funktionsgleichung in der Form <math>s(t) = A \cdot \sin (\omega t) </math>an! | # Gib die zugehörige Funktionsgleichung in der Form <math>s(t) = A \cdot \sin (\omega t) </math>an! | ||
:[[bild:FotoFederpendelZukunft_2b.png|700px]] }} | :[[bild:FotoFederpendelZukunft_2b.png|700px]] }} | ||
| − | ||{{#ev:youtube|O2-oE08wbk0|150}} | + | ||<!--{{#ev:youtube|O2-oE08wbk0|150}}--> |
|} | |} | ||
<!-- <ggb_applet height="540" width="730" filename="FotoFederpendelZukunft_2.ggb" /> <br> --> | <!-- <ggb_applet height="540" width="730" filename="FotoFederpendelZukunft_2.ggb" /> <br> --> | ||
| Zeile 56: | Zeile 62: | ||
# Betrachte den Graphen und überlege dir, inwiefern er nur fast der Graph einer Sinusfunktion ist! | # Betrachte den Graphen und überlege dir, inwiefern er nur fast der Graph einer Sinusfunktion ist! | ||
# Diskutiere was an dem Exerperiment "schief" gelaufen sein könnte!}} | # Diskutiere was an dem Exerperiment "schief" gelaufen sein könnte!}} | ||
| − | ||{{#ev:youtube|TAth1Hkqp-g|150}} | + | ||<!--{{#ev:youtube|TAth1Hkqp-g|150}}--> |
|} | |} | ||
| Zeile 71: | Zeile 77: | ||
Möchtest Du genaueres über das Oszilloskop wissen? Dann kannst Du Dich [http://www.elexs.de/oszi1.htm hier] freiwillig informieren. | Möchtest Du genaueres über das Oszilloskop wissen? Dann kannst Du Dich [http://www.elexs.de/oszi1.htm hier] freiwillig informieren. | ||
| − | ||{{#ev:youtube|IMVydCga8e0|150}} | + | ||<!--{{#ev:youtube|IMVydCga8e0|150}}--> |
|} | |} | ||
| Zeile 81: | Zeile 87: | ||
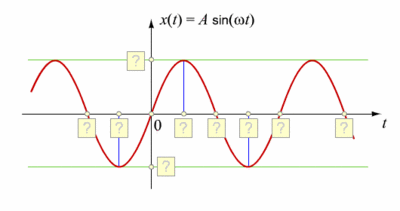
# Übernehme die folgende Zeichnung in dein Heft und vervollständige die Beschriftungen! | # Übernehme die folgende Zeichnung in dein Heft und vervollständige die Beschriftungen! | ||
:[[bild:Sinus.gif|left|400px]] }} | :[[bild:Sinus.gif|left|400px]] }} | ||
| − | ||{{#ev:youtube|JA2FuT_TB7c|150}} | + | ||<!--{{#ev:youtube|JA2FuT_TB7c|150}}--> |
|} | |} | ||
| Zeile 89: | Zeile 95: | ||
{{Arbeiten|NUMMER=P5 - Zusatzaufgabe|ARBEIT= | {{Arbeiten|NUMMER=P5 - Zusatzaufgabe|ARBEIT= | ||
Bearbeite diesen [http://www.mathe-online.at/lernpfade/harmonischeSchwingung/ Lernpfad] zur harmonischen Schwingung!}} | Bearbeite diesen [http://www.mathe-online.at/lernpfade/harmonischeSchwingung/ Lernpfad] zur harmonischen Schwingung!}} | ||
| − | ||{{#ev:youtube|F-jXwywnBtc|150}} | + | ||<!--{{#ev:youtube|F-jXwywnBtc|150}}--> |
|} | |} | ||
Aktuelle Version vom 29. März 2011, 00:03 Uhr
Einführung - Station 1: Einfluss der Parameter - Station 2: Bestimmung der Funktionsgleichung und mehr - Anwendungen
FAQ
Hier kannst du die Bedeutung der verwendeten Begriffe nachschlagen.
Anwendungen in der Physik
Methoden
- Wenn deine Klasse diese Station mit der Methode Arbeiten "im Pferdestall" bearbeiten möchte, klicke auf Arbeiten "im Pferdestall".
- Ansonsten ignoriere den genannten Link.
|
Hefteintrag: Formuliere eine Überschrift und mache dir Notizen zu den Aufgaben!
Es gibt viele periodische Vorgänge, also Vorgänge, die sich nach einer bestimmten Zeit wiederholen. Zeichnet man deren zeitlichen Verlauf auf, so erhält man einen sinusförmigen Graphen. |
| : |
|
|
| : |
|
Möchtest Du genaueres über das Oszilloskop wissen? Dann kannst Du Dich hier freiwillig informieren. |
|
|
Lösung zu Aufgabe Federpendel-Vokabelheft
Zurück zu Anwendungen!
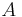 !
!
 ?
?
 !
!
 !
!
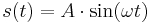 an!
an!