Exponentielles Wachstum - Lebensmittelkontrolle: Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | [[Bild:Agar_plate_with_colonies.jpg|miniatur|x150px|Petrischale zum Bakterienwachstumstest; Quelle: http://de.wikipedia.org]] | ||
In Österreich ist es üblich, dass Lebensmittel verarbeitende und verkaufende Betriebe der Lebensmittelkontrolle obliegen (siehe [http://www.bmg.gv.at/home/Schwerpunkte/VerbraucherInnengesundheit/Lebensmittel/ Bundesministerium für Gesundheit]). Lebensmittel dürfen nämlich einen bestimmten Grenzwert an Bakterien nicht überschreiten, wenn sie verkauft werden sollen. Lebensmittelkontrollore überwachen die korrekte Verwahrung der Speisen und Getränke. | In Österreich ist es üblich, dass Lebensmittel verarbeitende und verkaufende Betriebe der Lebensmittelkontrolle obliegen (siehe [http://www.bmg.gv.at/home/Schwerpunkte/VerbraucherInnengesundheit/Lebensmittel/ Bundesministerium für Gesundheit]). Lebensmittel dürfen nämlich einen bestimmten Grenzwert an Bakterien nicht überschreiten, wenn sie verkauft werden sollen. Lebensmittelkontrollore überwachen die korrekte Verwahrung der Speisen und Getränke. | ||
Egal um welche Art von Keimen es sich handelt, die Vermehrungsrate ist gigantisch. Aus diesem Grund verwendet man häufig eine Exponentialfunktion, um das Wachstum zu beschreiben. Mit Hilfe des Zusammenhangs <math>N(t)=a\cdot e^{b\cdot t}</math> lässt sich diese Wachstum beschreiben. | Egal um welche Art von Keimen es sich handelt, die Vermehrungsrate ist gigantisch. Aus diesem Grund verwendet man häufig eine Exponentialfunktion, um das Wachstum zu beschreiben. Mit Hilfe des Zusammenhangs <math>N(t)=a\cdot e^{b\cdot t}</math> lässt sich diese Wachstum beschreiben. | ||
| − | Diese Problem lässt sich mittel Differenzengleichung <math>N_{t+1}=N_{t}\cdot e^{b\cdot \tau}</math> modellieren, wobei <math>\tau</math> der Zeitschritt ist. Dies ist in der Tabellenkalkulationsmappe [[:Bild:Lebensmittel.xls '''Lebensmittel''']] (xls-Datei) realisiert. In der Arbeitsmappe befindet sich ein Arbeitsblatt, das zur Rückrechnung einer Keimanzahl verwendet werden kann. So kann überprüft werden, ob eine Lebensmittelprobe zum Zeitpunkt des Verkaufs noch genießbar war. | + | Diese Problem lässt sich mittel Differenzengleichung <math>N_{t+1}=N_{t}\cdot e^{b\cdot \tau}</math> modellieren, wobei <math>\tau</math> der Zeitschritt ist. Dies ist in der Tabellenkalkulationsmappe [[:Bild:Lebensmittel.xls| '''Lebensmittel''']] (xls-Datei, 85 kB) realisiert. In der Arbeitsmappe befindet sich ein Arbeitsblatt, das zur Rückrechnung einer Keimanzahl verwendet werden kann. So kann überprüft werden, ob eine Lebensmittelprobe zum Zeitpunkt des Verkaufs noch genießbar war. |
Es lassen sich die Anfangsanzahl der Keime sowie die Vermehrungskonstante variieren. Die Ergebnisse sind graphisch und in einer Tabelle dargestellt. | Es lassen sich die Anfangsanzahl der Keime sowie die Vermehrungskonstante variieren. Die Ergebnisse sind graphisch und in einer Tabelle dargestellt. | ||
| Zeile 12: | Zeile 13: | ||
| − | [[ | + | [[Von_der_diskreten_zur_kontinuierlichen_Veränderung#Themengebiete|Zurück zu Von der diskreten zur kontinuierlichen Veränderung]] |
Aktuelle Version vom 24. August 2011, 13:26 Uhr
In Österreich ist es üblich, dass Lebensmittel verarbeitende und verkaufende Betriebe der Lebensmittelkontrolle obliegen (siehe Bundesministerium für Gesundheit). Lebensmittel dürfen nämlich einen bestimmten Grenzwert an Bakterien nicht überschreiten, wenn sie verkauft werden sollen. Lebensmittelkontrollore überwachen die korrekte Verwahrung der Speisen und Getränke.
Egal um welche Art von Keimen es sich handelt, die Vermehrungsrate ist gigantisch. Aus diesem Grund verwendet man häufig eine Exponentialfunktion, um das Wachstum zu beschreiben. Mit Hilfe des Zusammenhangs 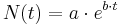 lässt sich diese Wachstum beschreiben.
lässt sich diese Wachstum beschreiben.
Diese Problem lässt sich mittel Differenzengleichung 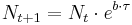 modellieren, wobei
modellieren, wobei 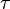 der Zeitschritt ist. Dies ist in der Tabellenkalkulationsmappe Lebensmittel (xls-Datei, 85 kB) realisiert. In der Arbeitsmappe befindet sich ein Arbeitsblatt, das zur Rückrechnung einer Keimanzahl verwendet werden kann. So kann überprüft werden, ob eine Lebensmittelprobe zum Zeitpunkt des Verkaufs noch genießbar war.
Es lassen sich die Anfangsanzahl der Keime sowie die Vermehrungskonstante variieren. Die Ergebnisse sind graphisch und in einer Tabelle dargestellt.
der Zeitschritt ist. Dies ist in der Tabellenkalkulationsmappe Lebensmittel (xls-Datei, 85 kB) realisiert. In der Arbeitsmappe befindet sich ein Arbeitsblatt, das zur Rückrechnung einer Keimanzahl verwendet werden kann. So kann überprüft werden, ob eine Lebensmittelprobe zum Zeitpunkt des Verkaufs noch genießbar war.
Es lassen sich die Anfangsanzahl der Keime sowie die Vermehrungskonstante variieren. Die Ergebnisse sind graphisch und in einer Tabelle dargestellt.
|
Merke:
Antibakterienvermehrungstheorem: |
Zurück zu Von der diskreten zur kontinuierlichen Veränderung


