Näherungsverfahren: Unterschied zwischen den Versionen
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Bisher wurde die Lösung der betrachteten Differentialgleichungen über '''Integration''' vorgestellt. | + | Bisher wurde die Lösung der betrachteten Differentialgleichungen über '''Integration''' vorgestellt. Mathematiker versuchen dabei, eine mathematisch '''exakte''' (und bis auf die Integrationskonstante eindeutige) '''Lösung''' formal zu bestimmen. Die gefundene Lösungsfunktion liefert eine vollständige Beschreibung des betrachteten Problems über den gesamten definierten Verlauf. In den meisten Fällen sind diese gefundenen Lösungsfunktionen auch stetig und bieten daher eine kontinuierliche Problemlösung.<br /> |
Es gibt aber viele Integrale und damit Differentialgleichungen, die man nur äußerst '''mühselig''' oder in vielen Fällen '''überhaupt nicht''' exakt lösen kann!<br /> | Es gibt aber viele Integrale und damit Differentialgleichungen, die man nur äußerst '''mühselig''' oder in vielen Fällen '''überhaupt nicht''' exakt lösen kann!<br /> | ||
| − | + | Mathematiker gehen daher oft den - nebenbei auch bei der Automatisation der Lösungsalgorithmen mit dem Computer meist schnelleren - Weg, die Probleme '''näherungsweise''' zu lösen. Sie setzen also auf Näherungsverfahren, die das vorliegende Problem für eine diskrete (endliche) Zahl von Punkten möglichst genau lösen. Sie ersetzen also die vollständige Integration einer Funktion durch die näherungsweise Berechnung (des bestimmten Integrals) in einem bestimmten Bereich, für den sie sich interessieren. Für diese Näherung / Diskretisierung gibt es verschiedene, unterschiedlich genaue - unterschiedlich komplexe Verfahren. | |
Grundsatz: | Grundsatz: | ||
| Zeile 13: | Zeile 13: | ||
Die bekanntesten Näherungsverfahren | Die bekanntesten Näherungsverfahren | ||
* [http://de.wikipedia.org/wiki/Eulersches_Polygonzugverfahren Euler-Cauchy-Verfahren] | * [http://de.wikipedia.org/wiki/Eulersches_Polygonzugverfahren Euler-Cauchy-Verfahren] | ||
| − | * Runge-Kutta-Verfahren | + | * [http://de.wikipedia.org/wiki/Newton-Verfahren Newton-Verfahren] |
| + | * [http://de.wikipedia.org/wiki/Runge-Kutta-Verfahren Runge-Kutta-Verfahren] | ||
| − | Eine Beschreibung der Verfahren | + | Eine Beschreibung der Verfahren findest Du bei [http://ifgivor.uni-muenster.de/vorlesungen/Num_Modellierung/Populat_Modelle/RungeKutta.html Ulrich Streit, Skript zur Übung "Werkzeuge zur numerischen Modellierung", 1999] |
| − | [[ | + | '''Beispiele:''' |
| + | * [[:Bild:Wachstum_exponentiell.wxm|<b>Exponentielles Wachstum - mit MAXIMA gelöst</b>]] (wxm-Datei, 2 kB) | ||
| + | * [[:Bild:Wachstum_logistisch.wxm|<b>Logistisches Wachstum - mit MAXIMA gelöst</b>]] (wxm-Datei, 2 kB) | ||
| + | |||
| + | Links:<br /> | ||
| + | * [http://www.acdca.ac.at/material/kl8/numerik.htm Josef Lechner, Von Euler-Cauchy zu Runge-Kutta, ACDCA, 1998] | ||
| + | * [http://education.ti.com/sites/DEUTSCHLAND/downloads/pdf/TI_Nachrichten_2_04.pdf Urs Oswald, H.R. Schneebeli, Kugelstoßen mit Luftwiderstand, TI-Nachrichten 2/04] (pdf-Datei, 2,2 MB) | ||
| + | * [http://www.kohorst-lemgo.de/modell/modlist.htm H. Kohorst, Ph. Portscheller, P. Goldkuhle, Modellbildung und Simulation - NRW-Bildungsserver learn:line] | ||
| + | |||
| + | |||
| + | [[Ausblick|Zurück zu Ausblick]] | ||
Aktuelle Version vom 24. August 2011, 13:29 Uhr
Bisher wurde die Lösung der betrachteten Differentialgleichungen über Integration vorgestellt. Mathematiker versuchen dabei, eine mathematisch exakte (und bis auf die Integrationskonstante eindeutige) Lösung formal zu bestimmen. Die gefundene Lösungsfunktion liefert eine vollständige Beschreibung des betrachteten Problems über den gesamten definierten Verlauf. In den meisten Fällen sind diese gefundenen Lösungsfunktionen auch stetig und bieten daher eine kontinuierliche Problemlösung.
Es gibt aber viele Integrale und damit Differentialgleichungen, die man nur äußerst mühselig oder in vielen Fällen überhaupt nicht exakt lösen kann!
Mathematiker gehen daher oft den - nebenbei auch bei der Automatisation der Lösungsalgorithmen mit dem Computer meist schnelleren - Weg, die Probleme näherungsweise zu lösen. Sie setzen also auf Näherungsverfahren, die das vorliegende Problem für eine diskrete (endliche) Zahl von Punkten möglichst genau lösen. Sie ersetzen also die vollständige Integration einer Funktion durch die näherungsweise Berechnung (des bestimmten Integrals) in einem bestimmten Bereich, für den sie sich interessieren. Für diese Näherung / Diskretisierung gibt es verschiedene, unterschiedlich genaue - unterschiedlich komplexe Verfahren.
Grundsatz: Der Differentialquotient wird näherungsweise durch den dazugehörigen Differenzenquotienten beschrieben.
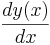beschrieben durch
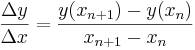
Die bekanntesten Näherungsverfahren
Eine Beschreibung der Verfahren findest Du bei Ulrich Streit, Skript zur Übung "Werkzeuge zur numerischen Modellierung", 1999
Beispiele:
- Exponentielles Wachstum - mit MAXIMA gelöst (wxm-Datei, 2 kB)
- Logistisches Wachstum - mit MAXIMA gelöst (wxm-Datei, 2 kB)
Links:
