Radioaktiver Zerfall - analytische Herleitung und Beispiele: Unterschied zwischen den Versionen
(→Beispiele zum radioaktiven Zerfall) |
|||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Die Gleichung <math>N(t)=N_{0} \cdot e^{-\lambda \cdot t}</math> ist eine der bekanntesten der Mathematik und wird in der zehnten Schulstufe eingeführt. In der zwölften Schulstufe ist es nun mit Hilfe der Integralrechung möglich, ausgehend vom Ansatz <math>N(t)'=-N(t) \cdot \lambda</math> obige Relation per Differentialgleichung analytisch herzuleiten. | + | Die Gleichung <math>N(t)=N_{0} \cdot e^{-\lambda \cdot t}</math> ist eine der bekanntesten der Mathematik und wird in der zehnten Schulstufe eingeführt. In der zwölften Schulstufe ist es Dir nun mit Hilfe der Integralrechung möglich, ausgehend vom Ansatz <math>N(t)'=-N(t) \cdot \lambda</math> obige Relation per Differentialgleichung analytisch herzuleiten. |
[[:Bild:Rad_zerfall_analytisch.pdf| '''Hier''']] (pdf-Datei, 85 kB) ist diese Herleitung Schritt für Schritt nachvollziehbar. Zuerst wird der allgemeine Fall besprochen und dann der Bezug auf die Anwendung beim radioaktiven Zerfall hergestellt. | [[:Bild:Rad_zerfall_analytisch.pdf| '''Hier''']] (pdf-Datei, 85 kB) ist diese Herleitung Schritt für Schritt nachvollziehbar. Zuerst wird der allgemeine Fall besprochen und dann der Bezug auf die Anwendung beim radioaktiven Zerfall hergestellt. | ||
| − | Zusätzlich sind drei Standardaufgaben angegeben, um die Verwendung der Gleichung zu wiederholen. | + | Zusätzlich sind für Dich drei Standardaufgaben angegeben, um Dir Möglichkeit zu geben, die Verwendung der Gleichung zu wiederholen. |
=== Beispiele zum radioaktiven Zerfall === | === Beispiele zum radioaktiven Zerfall === | ||
| Zeile 9: | Zeile 9: | ||
Der Zeitraum, in dem eine (meist exponentiell) abfallende Größe auf die Hälfte ihres Anfangswertes abgesunken ist. Die physikalische Halbwertszeit ist die für jedes Isotop eines radioaktiven Elementes charakteristische Zeitdauer, in der von einer ursprünglichen vorhandenen Anzahl radioaktiver Kerne bzw. instabilen Elementarteilchen die Hälfte zerfallen ist (entnommen aus ''Brockhaus in 5 Bänden'', zweiter Band). | Der Zeitraum, in dem eine (meist exponentiell) abfallende Größe auf die Hälfte ihres Anfangswertes abgesunken ist. Die physikalische Halbwertszeit ist die für jedes Isotop eines radioaktiven Elementes charakteristische Zeitdauer, in der von einer ursprünglichen vorhandenen Anzahl radioaktiver Kerne bzw. instabilen Elementarteilchen die Hälfte zerfallen ist (entnommen aus ''Brockhaus in 5 Bänden'', zweiter Band). | ||
}} | }} | ||
| + | |||
{{Arbeiten|NUMMER=1| | {{Arbeiten|NUMMER=1| | ||
| Zeile 14: | Zeile 15: | ||
Jod-131 hat eine Halbwertszeit von 8 Tagen. Berechne den Parameter λ (Basiszeiteinheit 1 Tag und 1 Jahr) in der Zerfallsgleichung auf 6 gültige Nachkommastellen! | Jod-131 hat eine Halbwertszeit von 8 Tagen. Berechne den Parameter λ (Basiszeiteinheit 1 Tag und 1 Jahr) in der Zerfallsgleichung auf 6 gültige Nachkommastellen! | ||
}} | }} | ||
| + | |||
{{Arbeiten|NUMMER=2| | {{Arbeiten|NUMMER=2| | ||
| Zeile 19: | Zeile 21: | ||
Von Kobalt-60 ist nach 3,88 Jahren 40% des Ausgangsmaterials zerfallen. Wie groß ist die Halbwertszeit dieses Isotops? | Von Kobalt-60 ist nach 3,88 Jahren 40% des Ausgangsmaterials zerfallen. Wie groß ist die Halbwertszeit dieses Isotops? | ||
}} | }} | ||
| + | |||
{{Arbeiten|NUMMER=3| | {{Arbeiten|NUMMER=3| | ||
| Zeile 24: | Zeile 27: | ||
Von 24000 Cäsium-137-Kernen sind nach einer bestimmten Zeit <math>\,t</math> 21771 Kerne zerfallen. Die Halbwertszeit des Isotops beträgt 2,1 Jahre. Berechne <math>\,t</math>! | Von 24000 Cäsium-137-Kernen sind nach einer bestimmten Zeit <math>\,t</math> 21771 Kerne zerfallen. Die Halbwertszeit des Isotops beträgt 2,1 Jahre. Berechne <math>\,t</math>! | ||
}} | }} | ||
| + | |||
'''Aufgaben im pdf-Format''' | '''Aufgaben im pdf-Format''' | ||
| Zeile 37: | Zeile 41: | ||
Die Lösungen zu diesen Aufgaben findet man unter: [[:Bild:Bsp_rad_zerfall_loes.pdf|'''Lösungen''']] (pdf-Datei, 59 kb). | Die Lösungen zu diesen Aufgaben findet man unter: [[:Bild:Bsp_rad_zerfall_loes.pdf|'''Lösungen''']] (pdf-Datei, 59 kb). | ||
| − | [[ | + | |
| + | [[Von_der_diskreten_zur_kontinuierlichen_Veränderung#Themengebiete|Zurück zu Von der diskreten zur kontinuierlichen Veränderung]] | ||
Aktuelle Version vom 24. August 2011, 14:27 Uhr
Die Gleichung 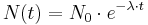 ist eine der bekanntesten der Mathematik und wird in der zehnten Schulstufe eingeführt. In der zwölften Schulstufe ist es Dir nun mit Hilfe der Integralrechung möglich, ausgehend vom Ansatz
ist eine der bekanntesten der Mathematik und wird in der zehnten Schulstufe eingeführt. In der zwölften Schulstufe ist es Dir nun mit Hilfe der Integralrechung möglich, ausgehend vom Ansatz 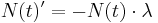 obige Relation per Differentialgleichung analytisch herzuleiten.
Hier (pdf-Datei, 85 kB) ist diese Herleitung Schritt für Schritt nachvollziehbar. Zuerst wird der allgemeine Fall besprochen und dann der Bezug auf die Anwendung beim radioaktiven Zerfall hergestellt.
obige Relation per Differentialgleichung analytisch herzuleiten.
Hier (pdf-Datei, 85 kB) ist diese Herleitung Schritt für Schritt nachvollziehbar. Zuerst wird der allgemeine Fall besprochen und dann der Bezug auf die Anwendung beim radioaktiven Zerfall hergestellt.
Zusätzlich sind für Dich drei Standardaufgaben angegeben, um Dir Möglichkeit zu geben, die Verwendung der Gleichung zu wiederholen.
Beispiele zum radioaktiven Zerfall
|
Merke:
Halbwertszeit: Der Zeitraum, in dem eine (meist exponentiell) abfallende Größe auf die Hälfte ihres Anfangswertes abgesunken ist. Die physikalische Halbwertszeit ist die für jedes Isotop eines radioaktiven Elementes charakteristische Zeitdauer, in der von einer ursprünglichen vorhandenen Anzahl radioaktiver Kerne bzw. instabilen Elementarteilchen die Hälfte zerfallen ist (entnommen aus Brockhaus in 5 Bänden, zweiter Band). |
|
Jod-131 hat eine Halbwertszeit von 8 Tagen. Berechne den Parameter λ (Basiszeiteinheit 1 Tag und 1 Jahr) in der Zerfallsgleichung auf 6 gültige Nachkommastellen! |
|
Von Kobalt-60 ist nach 3,88 Jahren 40% des Ausgangsmaterials zerfallen. Wie groß ist die Halbwertszeit dieses Isotops? |
|
Von 24000 Cäsium-137-Kernen sind nach einer bestimmten Zeit |
Aufgaben im pdf-Format
Die Angaben zu den Aufgaben findet man hier (pdf-Datei, 43 kb).
Lösungen im pdf-Format
Die Lösungen zu diesen Aufgaben findet man unter: Lösungen (pdf-Datei, 59 kb).
Zurück zu Von der diskreten zur kontinuierlichen Veränderung

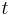 21771 Kerne zerfallen. Die Halbwertszeit des Isotops beträgt 2,1 Jahre. Berechne
21771 Kerne zerfallen. Die Halbwertszeit des Isotops beträgt 2,1 Jahre. Berechne 
