Quadratische Funktionen - Teste dein Wissen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> [[Einführung_in_quadratische_F...) |
K (hat „Quadratische Funktionen/ Teste dein Wissen“ nach „Quadratische Funktionen - Teste dein Wissen“ verschoben und dabei eine Weiterleitung überschrieben: zurück verschieben) |
||
| (6 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
== Interaktive Übungen == | == Interaktive Übungen == | ||
| − | + | Im vorigen Kapitel hatten wir es mit einer Funktion zu tun, die neben dem reinquadratischen Teil (dem Bremsweg) auch noch einen linearen Teil (den Reaktionsweg) besaß. | |
| + | Den allgemeinsten Fall einer quadratischen Funktion haben wir, wenn die Funktionsgleichung die Form <span style="background-color:yellow;"> '''<math>f(x)=ax^2+bx+c </math>''' </span> hat. | ||
| + | |||
| + | An Funktionen mit derartigen Gleichungen sollst du nun dein Wissen erproben: | ||
| + | |||
| + | {{Arbeiten| | ||
| + | NUMMER=1| | ||
| + | ARBEIT= | ||
| + | Experimentiere mit dem Applet und erläutere, welchen Einfluss die Parameter a, b und c auf den Verlauf des Graphen haben. | ||
| + | |||
| + | }} | ||
| + | |||
| + | <ggb_applet height="400" width="950" filename="Parabeln_test.ggb" /> | ||
| + | |||
| + | |||
| + | {{Arbeiten| | ||
| + | NUMMER=2| | ||
| + | ARBEIT= | ||
| + | Stelle die drei Schieberegler so ein, dass der schwarze Graph genau auf dem | ||
| + | |||
| + | '''a)''' roten | ||
| + | |||
| + | '''b)''' grünen | ||
| + | |||
| + | '''c)''' blauen | ||
| + | |||
| + | Graphen liegt. | ||
| + | |||
| + | }} | ||
| + | |||
| + | <ggb_applet height="550" width="950" filename="Parabeln.ggb" /> | ||
| + | |||
| + | {{Arbeiten| | ||
| + | NUMMER=3| | ||
| + | ARBEIT= | ||
| + | In den Aufgaben '''2b)''' und '''c)''' hast du wahrscheinlich einen Zusammenhang (''"Wenn zwei Graphen spiegelbildlich bezüglich der y-Achse liegen, dann ..."'') entdeckt. | ||
| + | Experimentiere erneut mit dem ersten Applet und bestätige deine Vermutung. | ||
| + | }} | ||
== Arbeitsblätter == | == Arbeitsblätter == | ||
| Zeile 18: | Zeile 55: | ||
| − | + | ||
| − | + | *Allgemeine Überlegungen | |
| − | + | Term -> Graph - Graph -> Term [Geogebra-Schieberegler] - Nullstellen - Scheitel | |
| − | + | ||
| | ||
{{Autoren|[[Benutzer:Reinhard Schmidt|Reinhard Schmidt]], [[Benutzer:Christian Schmidt|Christian Schmidt]], [[Benutzer:Maria Eirich|Maria Eirich]], [[Benutzer:Andrea Schellmann|Andrea Schellmann]] und [[Benutzer:Gabi Jauck|Gabi Jauck]]}} | {{Autoren|[[Benutzer:Reinhard Schmidt|Reinhard Schmidt]], [[Benutzer:Christian Schmidt|Christian Schmidt]], [[Benutzer:Maria Eirich|Maria Eirich]], [[Benutzer:Andrea Schellmann|Andrea Schellmann]] und [[Benutzer:Gabi Jauck|Gabi Jauck]]}} | ||
Aktuelle Version vom 4. Januar 2011, 12:41 Uhr
Einführung - Bremsweg - Unterschiedliche Straßenverhältnisse - Übungen - Anhalteweg - Teste dein Wissen!
Interaktive Übungen
Im vorigen Kapitel hatten wir es mit einer Funktion zu tun, die neben dem reinquadratischen Teil (dem Bremsweg) auch noch einen linearen Teil (den Reaktionsweg) besaß.
Den allgemeinsten Fall einer quadratischen Funktion haben wir, wenn die Funktionsgleichung die Form 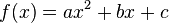 hat.
hat.
An Funktionen mit derartigen Gleichungen sollst du nun dein Wissen erproben:
|
Experimentiere mit dem Applet und erläutere, welchen Einfluss die Parameter a, b und c auf den Verlauf des Graphen haben. |
|
Stelle die drei Schieberegler so ein, dass der schwarze Graph genau auf dem a) roten b) grünen c) blauen Graphen liegt. |
|
In den Aufgaben 2b) und c) hast du wahrscheinlich einen Zusammenhang ("Wenn zwei Graphen spiegelbildlich bezüglich der y-Achse liegen, dann ...") entdeckt. Experimentiere erneut mit dem ersten Applet und bestätige deine Vermutung. |
Arbeitsblätter
Links
- Allgemeine Überlegungen
Term -> Graph - Graph -> Term [Geogebra-Schieberegler] - Nullstellen - Scheitel
|
Dieser Lernpfad wurde erstellt von:
Reinhard Schmidt, Christian Schmidt, Maria Eirich, Andrea Schellmann und Gabi Jauck |


