Potenzfunktionen - 2. Stufe: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 1: | Zeile 1: | ||
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | ||
| − | + | [[Potenzfunktionen|Start]] -[[Potenzfunktionen_Einführung|Einführung]] - [[Potenzfunktionen_1. Stufe|1. Stufe]] - [[Potenzfunktionen_2. Stufe|2. Stufe]] - [[Potenzfunktionen_3. Stufe|3. Stufe]] - [[Potenzfunktionen_4. Stufe|4. Stufe]] - [[Potenzfunktionen_5. Stufe|5. Stufe]] | |
| + | </div> | ||
| − | + | == Die Graphen der Funktionen mit f(x) = x<sup>-n</sup>, n <small>∈</small> IN == | |
| − | == Die Graphen der Funktionen mit f(x) = x<sup>-n</sup>, n | + | === Gerade Potenzen === |
| − | + | ||
| − | < | + | |
| − | < | + | |
| − | + | ||
| − | + | ||
| − | < | + | '''Wir betrachten zunächst die Graphen der Funktionen mit f(x) = x<sup>-n</sup>, wenn n eine gerade Zahl ist, also n = 2, 4, 6, ...''' |
| − | {{Arbeiten|NUMMER=1|ARBEIT= | + | |
| − | # | + | {| cellspacing="10" |
| − | # Beschreibe die Veränderung der Graphen beim Übergang von f(x) = x<sup>-2</sup> zu f(x) = x<sup>-4</sup>, dann die | + | |- style="vertical-align:top;" |
| − | + | | {{Arbeiten|NUMMER=1|ARBEIT= | |
| + | # Mit dem Schieberegler kannst du den Exponenten verändern. Beschreibe Gemeinsamkeiten und Unterschiede der Graphen! Achte dabei auf | ||
| + | #* Symmetrie | ||
| + | #* Monotonie | ||
| + | #* größte und kleinste Funktionswerte | ||
| + | # Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe! Zur Hilfe kannst du auch die Schar der Graphen zeichnen lassen. <br> <pre>HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen </pre> | ||
| + | # Beschreibe die Veränderung der Graphen beim Übergang von f(x) = x<sup>-2</sup> zu f(x) = x<sup>-4</sup>, dann die beim Übergang von f(x) = x<sup>-4</sup> zu f(x) = x<sup>-6</sup> usw.! | ||
| + | # Wie ändern sich die y-Werte bei f(x) = x<sup>-n</sup>, n gerade, wenn der x-Wert ver-k-facht wird? | ||
| + | :{{Lösung versteckt| | ||
| + | :Wenn der x-Wert ver-k-facht wird, dann wird der y-Wert ver-<math>\frac 1k</math>-facht. <br> | ||
| + | :Symbolisch <math>f(k \cdot x) = (kx)^{-n} = k^{-n} \cdot x^{-n} = \frac 1k \cdot f(x)</math>. | ||
}} | }} | ||
| − | <br> | + | }}<br> |
| + | || <ggb_applet height="300" width="350" showMenuBar="false" showResetIcon="true" | ||
| + | filename="3_gerade_xn.ggb" /> | ||
| + | |} | ||
| − | + | === Ungerade Potenzen === | |
| − | + | ||
| − | < | + | '''Wir betrachten nun die Graphen der Funktionen mit f(x) = x<sup>n</sup>, wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..''' |
| − | {{Arbeiten|NUMMER= | + | |
| − | # | + | {| <!--class="prettytable sortable" --> |
| − | + | |- style="vertical-align:top;" | |
| − | ! | + | | <ggb_applet height="300" width="350" showMenuBar="false" showResetIcon="true" |
| + | filename="3_ungerade_xn.ggb" /> | ||
| + | || | ||
| + | {{Arbeiten|NUMMER=2|ARBEIT= | ||
| + | # Beschreibe wieder die Graphen! Achte dabei auf | ||
| + | #* Symmetrie | ||
| + | #* Monotonie | ||
| + | #* größte und kleinste Funktionswerte | ||
| + | # Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe!<br><pre>HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen</pre> | ||
| + | # Beschreibe die Veränderung der Graphen beim Übergang von f(x) = x<sup>1</sup> zu f(x) = x<sup>3</sup>, dann die beim Übergang von f(x) = x<sup>3</sup> zu f(x) = x<sup>5</sup> usw.! | ||
}} | }} | ||
| + | |} | ||
| + | |||
| + | === Teste dein Wissen === | ||
| + | {{Arbeiten|NUMMER=3|ARBEIT= | ||
| + | Wir betrachten die Funktionen mit f(x) = x<sup>n</sup>, n eine natürliche Zahl | ||
| + | # Für welches n verläuft der Graph durch den Punkt P(2;32)? | ||
| + | # Für welches n verläuft der Graph durch Q(1,5;3,375)? | ||
| + | :{{Lösung versteckt| | ||
| + | :Der Punkt P(2;32) wird für <math>n=5</math> durchlaufen: <math>f \left( 2 \right ) = 2^5 = 32</math>.<br> | ||
| + | :Der Punkt Q(1,5;3,375) wird für <math>n=3</math> durchlaufen: <math>f \left( 1,5 \right ) = 2^3 = 3,375</math>. | ||
| + | }} | ||
| + | }} | ||
| + | |||
| + | == Die Graphen von f(x) = a*x<sup>n</sup>, mit a <small>∈</small> IR == | ||
| + | |||
| + | '''Wir betrachten jetzt die Funktionen mit f(x) = a*x<sup>n</sup>, wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n <small>∈</small> IN, a <small>∈</small> IR .''' | ||
| + | |||
| + | {| <!--class="prettytable sortable"--> | ||
| + | |- style="vertical-align:top;" | ||
| + | | {{Arbeiten|NUMMER=4|ARBEIT= | ||
| + | # Es sei zunächst n = 2, also <math>f(x) = a \cdot x^2</math>. Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a! | ||
| + | # Beschreibe die Veränderung der Graphen mit <math>f(x) = a \cdot x^n </math> bei der Veränderung des Parameter a! Unterscheide dabei wieder zwischen geraden und ungeraden Exponenten. | ||
| + | }} | ||
| + | || <ggb_applet height="300" width="350" showMenuBar="false" showResetIcon="true" | ||
| + | filename="4_axn.ggb" /> | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | {| <!--class="prettytable sortable"--> | ||
| + | |- style="vertical-align:top;" | ||
| + | | <ggb_applet height="350" width="450" showMenuBar="false" showResetIcon="true" | ||
| + | filename="4_axn_test.ggb" /> | ||
| + | || | ||
| + | {{Arbeiten|NUMMER=5|ARBEIT= | ||
| + | Wir betrachten wieder die Funktionen mit <math>f(x) = a \cdot x^n</math>, n eine natürliche Zahl | ||
| + | # Bestimme a und n so, dass der Graph durch die Punkte A(-2;4) und B(1;-0,5) verläuft. Nebenstehende Graphik dient als Hilfe. Die Punkte A und B kannst du frei verschieben. | ||
| + | # Bestimme a und n so, dass der Graph durch die Punkte A(-1;-1) und B(0,5;3) verläuft. Was fällt auf? Erkläre deine Beobachtungen. | ||
| + | :{{Lösung versteckt| | ||
| + | : 1. <math>a = -0.5, n = 3</math><br> | ||
| + | : 2. Es gibt keine Lösung, denn ...}} | ||
| + | }}<br> | ||
| + | |||
| + | |} | ||
| + | |||
| + | === Teste Dein Wissen === | ||
| + | |||
| + | * [http://www.realmath.de/Neues/Klasse10/potenzfunktion/ggbxhochn.html Betrachte den Graphen und finde die richtigen Aussagen!] | ||
| + | * [http://www.realmath.de/Neues/Klasse10/potenzfunktion/defpotquiz.html Ordne dem Graphen der Potenzfunktion die richtige Gleichung zu!] | ||
Version vom 15. Januar 2009, 19:46 Uhr
Inhaltsverzeichnis |
Die Graphen der Funktionen mit f(x) = x-n, n ∈ IN
Gerade Potenzen
Wir betrachten zunächst die Graphen der Funktionen mit f(x) = x-n, wenn n eine gerade Zahl ist, also n = 2, 4, 6, ...
|
Ungerade Potenzen
Wir betrachten nun die Graphen der Funktionen mit f(x) = xn, wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..
|
Teste dein Wissen
|
Wir betrachten die Funktionen mit f(x) = xn, n eine natürliche Zahl
|
Die Graphen von f(x) = a*xn, mit a ∈ IR
Wir betrachten jetzt die Funktionen mit f(x) = a*xn, wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n ∈ IN, a ∈ IR .
|
|
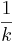 -facht.
-facht. 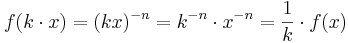 .
.
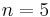 durchlaufen:
durchlaufen: 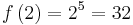 .
.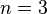 durchlaufen:
durchlaufen: 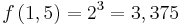 .
.
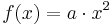 . Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
. Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
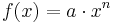 bei der Veränderung des Parameter a! Unterscheide dabei wieder zwischen geraden und ungeraden Exponenten.
bei der Veränderung des Parameter a! Unterscheide dabei wieder zwischen geraden und ungeraden Exponenten.