Bestimmung der Funktionsgleichung aus dem Graphen: Unterschied zwischen den Versionen
K (→Bestimmung einer Funktionsgleichung aus dem Graphen) |
K (→Bestimmung einer Funktionsgleichung aus dem Graphen) |
||
| Zeile 52: | Zeile 52: | ||
Nullstellen: <math>x_N = \frac{1}{3}\pi+k\cdot \frac{\pi}{2} </math> mit <math>\ k \in \Z</math> oder <math>x_N \in \{ ...; -\frac{1}{6}\pi;\ \frac{1}{3}\pi;\ \frac{5}{6}\pi;\ \frac{4}{3}\pi;\ \frac{5}{3}\pi;\ ...\}</math> | Nullstellen: <math>x_N = \frac{1}{3}\pi+k\cdot \frac{\pi}{2} </math> mit <math>\ k \in \Z</math> oder <math>x_N \in \{ ...; -\frac{1}{6}\pi;\ \frac{1}{3}\pi;\ \frac{5}{6}\pi;\ \frac{4}{3}\pi;\ \frac{5}{3}\pi;\ ...\}</math> | ||
| − | Tiefpunkte: <math>x_T = \frac{7}{12}\pi + k \cdot \pi</math> mit <math>\ k \in \Z</math> oder <math>x_T \in \{ ...; | + | Tiefpunkte: <math>x_T = \frac{7}{12}\pi + k \cdot \pi</math> mit <math>\ k \in \Z</math> oder <math>x_T \in \{ ...; -\frac{5}{12}\pi;\ \frac{7}{12}\pi;\ \frac{19}{12}\pi;...}</math> |
Version vom 16. Januar 2009, 23:36 Uhr
Einführung - Einfluss der Parameter - Bestimmung der Funktionsgleichung aus dem Graphen - Anwendungen in der Physik - Zusatzaufgaben
Informationen aus dem Graphen
|
|
|
Bestimmung einer Funktionsgleichung aus dem Graphen
Man kann aus dem Graphen einer Funktion eine zugehörige Funktionsgleichung bestimmen. Um zu sehen wie, klicke in das leere Kontrollkästchen.
Jetzt noch was zum Knobeln!!!
(Arbeitsanweisungen fehlen noch.)
|
Lösung zu Aufgabe 1:
Amplitude: 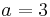
Wertemenge: ![W = [-3;\ 3]](/images/math/7/f/4/7f4a584468ac15313bbdcbd41602ca3e.png)
Periode: 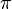
Nullstellen: 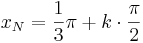 mit
mit  oder
oder 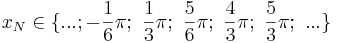
Tiefpunkte: 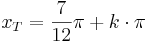 mit
mit  oder Fehler beim Parsen(Syntaxfehler): x_T \in \{ ...; -\frac{5}{12}\pi;\ \frac{7}{12}\pi;\ \frac{19}{12}\pi;...}
oder Fehler beim Parsen(Syntaxfehler): x_T \in \{ ...; -\frac{5}{12}\pi;\ \frac{7}{12}\pi;\ \frac{19}{12}\pi;...}
Lösung zu Aufgabe 2:
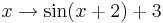 und
und 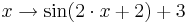
Weiter geht es mit

