Potenzfunktionen - 2. Stufe: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 79: | Zeile 79: | ||
|| | || | ||
{{Arbeiten|NUMMER=5|ARBEIT= | {{Arbeiten|NUMMER=5|ARBEIT= | ||
| − | |||
| − | |||
Wir betrachten wieder die Funktionen mit <math>f(x) = a \cdot x^{-n}</math>, n eine natürliche Zahl | Wir betrachten wieder die Funktionen mit <math>f(x) = a \cdot x^{-n}</math>, n eine natürliche Zahl | ||
| − | # Bestimme a und n so, dass der Graph durch die Punkte A(- | + | # Bestimme a und n so, dass der Graph durch die Punkte A(-1;-2) und B(2;1) verläuft. Nebenstehende Graphik dient als Hilfe. Die Punkte A und B kannst du frei verschieben. |
| − | # Bestimme a und n so, dass der Graph durch die Punkte A(-1;-1) und B( | + | # Bestimme a und n so, dass der Graph durch die Punkte A(-1;-1) und B(1;3) verläuft. Was fällt auf? Erkläre deine Beobachtungen. |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | + | # <math>a = 2, n = 1</math>. | |
| + | # Hier gibt es wegen der Symmetrie des Graphen keine Lösungen.}} | ||
}}<br> | }}<br> | ||
Version vom 22. Januar 2009, 15:51 Uhr
Inhaltsverzeichnis |
Die Graphen der Funktionen mit f(x) = x-n, n ∈ IN
Gerade Potenzen
Wir betrachten zunächst die Graphen der Funktionen mit f(x) = x-n, wenn n eine gerade Zahl ist, also n = 2, 4, 6, ...
|
Ungerade Potenzen
Wir betrachten nun die Graphen der Funktionen mit 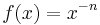 , wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..
, wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..
|
Teste dein Wissen
|
TODO: Neue Aufgaben (?)
|
Die Graphen von f(x) = a*x-n, mit a ∈ IR
Wir betrachten jetzt die Funktionen mit 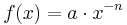 , wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n ∈ IN, a ∈ IR .
, wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n ∈ IN, a ∈ IR .
|
|
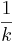 -facht.
-facht. 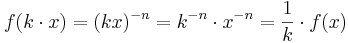 .
.
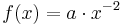 . Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
. Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
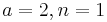 .
.

