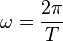Anwendungen in der Physik: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
K (→Anwendungen in der Physik) |
K (→Anwendungen in der Physik) |
||
| Zeile 6: | Zeile 6: | ||
===Anwendungen in der Physik=== | ===Anwendungen in der Physik=== | ||
| − | {{Arbeit|ARBEIT=Die Möve hängt an einer Feder und schwingt bei einmaliger Auslenkung. Im Bild sind die Ruhelage und die größten Auslenkungen aus dieser zu sehen. Die Zeitabstände zwischen den einzelnen Fotos sind jeweils gleich groß. . | + | {{Arbeit|ARBEIT=Die Möve hängt an einer Feder und schwingt bei einmaliger Auslenkung. Im Bild sind die Ruhelage und die größten Auslenkungen aus dieser zu sehen. Die Zeitabstände zwischen den einzelnen Fotos sind jeweils gleich groß. |
| + | # Bestimme die Amplitude! | ||
| + | # Wie groß ist die Schwingungsdauer? | ||
| + | # Wie viele Perioden pro Sekunde gibt es? Diese Anzahl wird auch als Frequenz bezeichnet. | ||
| + | # Gib die zugehörige Funktionsgleichung in der Form <math>s(t) = A \cdot \sin (\omega t) </math>an!}} | ||
{{Merksatz|MERK= | {{Merksatz|MERK= | ||
| Zeile 21: | Zeile 25: | ||
:Als Frequenz bezeichnet man die Anzahl der Schwingungen pro Sekunde | :Als Frequenz bezeichnet man die Anzahl der Schwingungen pro Sekunde | ||
* Kreisfrequenz <math>\omega</math> ("omega") | * Kreisfrequenz <math>\omega</math> ("omega") | ||
| + | :<math>\omega = \frac{2\pi}{T}</math> | ||
}} | }} | ||
Version vom 21. Januar 2009, 16:46 Uhr
Einführung - Einfluss der Parameter - Bestimmung der Funktionsgleichung aus dem Graphen - Anwendungen in der Physik - Zusatzaufgaben
Anwendungen in der Physik
|
Die Möve hängt an einer Feder und schwingt bei einmaliger Auslenkung. Im Bild sind die Ruhelage und die größten Auslenkungen aus dieser zu sehen. Die Zeitabstände zwischen den einzelnen Fotos sind jeweils gleich groß.
|
|
Merke:
wichtige Begriffe:
|
Wiederholung: Frequenz und Amplitude
|
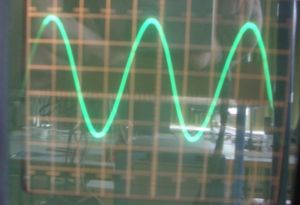
Auf einem Oszilloskop sieht man obiges Bild.
|
a) Die Sinuskurve ist um 0,75 nach oben verschoben.
Der Abstand zwischen Hoch- und Tiefpunkt der Sinuslinie ist 4,5, also ist die Amplitude 2,25.
Die Periodendauer ist 3,75.
Die Sinuskurve fängt mit 0,25 am linken Rand an.
b) Es sind d = 0,75, a = 2,25, b = 2*PI/3,75 und c = -0,224.
|
Weiter geht es mit
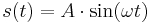 an!
an!

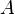
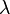 ("lambda")
("lambda")

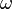 ("omega")
("omega")