Potenzfunktionen - 2. Stufe: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 20: | Zeile 20: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
:Wenn der x-Wert ver-k-facht wird, dann wird der y-Wert ver-<math>\frac {1}{k^n}</math>-facht. <br> | :Wenn der x-Wert ver-k-facht wird, dann wird der y-Wert ver-<math>\frac {1}{k^n}</math>-facht. <br> | ||
| − | :Symbolisch <math>f(k \cdot x) = (kx)^{-n} = k^{-n} \cdot x^{-n} = \frac | + | :Symbolisch <math>f(k \cdot x) = (kx)^{-n} = k^{-n} \cdot x^{-n} = \frac {1}{k^n} \cdot f(x)</math>. |
}} | }} | ||
}}<br> | }}<br> | ||
Version vom 24. Januar 2009, 19:12 Uhr
Inhaltsverzeichnis |
Die Graphen der Funktionen mit f(x) = x-n, n ∈ IN
Gerade Potenzen
Wir betrachten zunächst die Graphen der Funktionen mit f(x) = x-n, wenn n eine gerade Zahl ist, also n = 2, 4, 6, ...
|
Ungerade Potenzen
Wir betrachten nun die Graphen der Funktionen mit 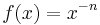 , wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..
, wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..
|
Teste dein Wissen
|
Wir betrachten die Funktionen mit f(x) = x-n, n eine natürliche Zahl
|
Die Graphen von f(x) = a*x-n, mit a ∈ IR
Wir betrachten jetzt die Funktionen mit 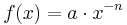 , wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n ∈ IN, a ∈ IR .
, wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n ∈ IN, a ∈ IR .
|
|
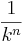 -facht.
-facht. 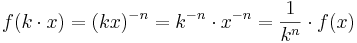 .
.
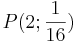
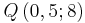 ?
?
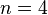 , dann gilt nämlich
, dann gilt nämlich 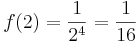 .
.
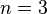 , dann gilt nämlich
, dann gilt nämlich 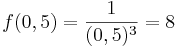
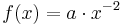 . Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
. Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
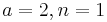 .
.

