Potenzfunktionen - 4. Stufe: Unterschied zwischen den Versionen

Aus Medienvielfalt-Wiki
Wechseln zu: Navigation, Suche
K (→‎Vergleich mit Funktionen aus Stufe 3)
Zeile 8: Zeile 8:
  
 
=== Vergleich mit Funktionen aus Stufe 3 ===
 
=== Vergleich mit Funktionen aus Stufe 3 ===
 +
 +
{| cellspacing="10"
 +
|- style="vertical-align:top;"
 +
| {{Arbeiten|NUMMER=1|ARBEIT=
 +
Verleiche den neuen Graphen (blau) mit dem, den Du schon aus Stufe 3 dieses Kurses kennst (rot gestrichelt); mit dem Schieberegler kannst Du dazu wieder die Exponenten verändern.
 +
# Beschreibe Gemeinsamkeiten und Unterschiede der Graphen! Achte dabei auf
 +
#* Definitionsbereich
 +
#* Symmetrie
 +
#* Monotonie
 +
#* größte und kleinste Funktionswerte
 +
# Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe! Zur Hilfe kannst du auch die Schar der Graphen zeichnen lassen. <br> <pre>HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen </pre>
 +
:{{Lösung versteckt|
 +
:Wenn der x-Wert ver-k-facht wird, dann wird der y-Wert ver-k<sup>n</sup>-facht. <br>
 +
:Symbolisch <math>f(k \cdot x) = (kx)^n = k^n \cdot x^n = k^n \cdot f(x)</math>.
 +
}}
 +
}}<br>
 +
|| <ggb_applet height="300" width="550" showMenuBar="false" showResetIcon="true"
 +
filename="w_xm1n.ggb" />
 +
|}
 +
 +
{{ggb|w_xm1n.ggb|datei}}
 +
 +
 +
 +
 +
 +
 +
 +
 +
 +
  
 
<ggb_applet height="450" width="600" showMenuBar="false" showResetIcon="true"  
 
<ggb_applet height="450" width="600" showMenuBar="false" showResetIcon="true"  

Version vom 28. Januar 2009, 17:19 Uhr

Start - Einführung - 1. Stufe - 2. Stufe - 3. Stufe - 4. Stufe - 5. Stufe

Die Graphen der Funktionen mit f(x) = x-1/n, n ∈ IN

Es sei stets IN0={0,1,2,...} und IN={1,2,3,..}, insbesondere also IN0 =/= IN.
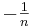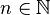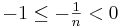Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen negativen Stammbruch der Form \textstyle - \frac{1}{n} mit n \in \mathbb{N} als Exponenten haben. Für diese Art der Exponenten gilt: -1\leq \textstyle -\frac{1}{n}< 0.

Vergleich mit Funktionen aus Stufe 3

  Aufgabe 1  Stift.gif

Verleiche den neuen Graphen (blau) mit dem, den Du schon aus Stufe 3 dieses Kurses kennst (rot gestrichelt); mit dem Schieberegler kannst Du dazu wieder die Exponenten verändern.

  1. Beschreibe Gemeinsamkeiten und Unterschiede der Graphen! Achte dabei auf
    • Definitionsbereich
    • Symmetrie
    • Monotonie
    • größte und kleinste Funktionswerte
  2. Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe! Zur Hilfe kannst du auch die Schar der Graphen zeichnen lassen. 
    HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen
Wenn der x-Wert ver-k-facht wird, dann wird der y-Wert ver-kn-facht.
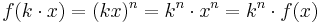Symbolisch f(k \cdot x) = (kx)^n = k^n \cdot x^n = k^n \cdot f(x).


Geogebra.png datei









Von „http://medienvielfalt.zum.de/index.php?title=Potenzfunktionen_-_4._Stufe&oldid=2122“