Potenzfunktionen - 4. Stufe: Unterschied zwischen den Versionen
K |
K |
||
| Zeile 50: | Zeile 50: | ||
}} | }} | ||
|} | |} | ||
| + | |||
| + | == Funktionen und ihre Umkehrfunktionen == | ||
| + | |||
| + | ???? | ||
| + | |||
| + | |||
<ggb_applet height="450" width="600" showMenuBar="false" showResetIcon="true" | <ggb_applet height="450" width="600" showMenuBar="false" showResetIcon="true" | ||
filename="10_axminuas1nc.ggb" /> | filename="10_axminuas1nc.ggb" /> | ||
Version vom 28. Januar 2009, 21:15 Uhr
Inhaltsverzeichnis |
Die Graphen der Funktionen mit f(x) = x-1/n, n ∈ IN
Es sei stets IN0={0,1,2,...} und IN={1,2,3,..}, insbesondere also IN0 =/= IN.
Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen negativen Stammbruch der Form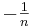 
mit 
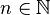als Exponenten haben. Für diese Art der Exponenten gilt: 
.
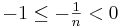Vergleich mit Funktionen aus Stufe 3
|
Exponenten, Brüche und Potenzgesetze
Im vorliegenden Fall betrachten wir negative Stammbrüche als Exponten. Man erinnere sich dabei an die Potenzgesetze, insbesondere an folgenden Zusammenhang:
- Für eine reelle Zahl
und eine natürliche Zahl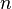 
wird definiert:
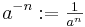für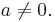 
Auf unsere Situation angewandt ergibt sich:
|
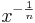
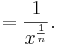
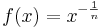den Definitonsbereich D = IR+.
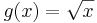nur auf IR+ definiert, das heißt ihr Definitionsbereich 
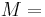IR+.![f(x) = x^{-\frac 1 n}= \textstyle \frac{1}{x^{\frac 1 n}} = \textstyle \frac{1}{\sqrt[n]{x}} = \textstyle \frac{1}{g(x)}](/images/math/d/f/f/dffb5aedde565c318a02642cbcd56b38.png)
überträgt sich der Definitionsbereich der Funktion g auf die Funktion f.Funktionen und ihre Umkehrfunktionen
????
