Potenzfunktionen - 5. Stufe: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(1. Aufgabe geändert) |
(Aufgabe 1 geändert) |
||
| Zeile 17: | Zeile 17: | ||
#* Symmetrie | #* Symmetrie | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | :* | + | :*Ist der Nenner im vollständig gekürzten Bruch gerade, so ist der Definitionsbereich auf <math>\mathbb{R}^{+}</math> eingeschränkt. Bei allen anderen Funktionen ist der Definitionsbereich <math>\mathbb{R}</math>. |
| − | * Wenn der Exponent vollständig gekürzt | + | :* Wenn der Exponent vollständig gekürzt |
| − | ** einen geraden Zähler besitzt, ist der Graph der Funktion achsensymmetrisch.<br> | + | :** einen geraden Zähler besitzt, ist der Graph der Funktion achsensymmetrisch.<br> |
| − | ** einen geraden Nenner besitzt, ist der Graph nicht symmetrisch, da nur für <math>\mathbb{R}</math> definiert. | + | :** einen geraden Nenner besitzt, ist der Graph nicht symmetrisch, da nur für <math>\mathbb{R}</math> definiert. |
| − | ** ungeraden Zähler und Nenner besitzt, ist der Graph punktsymmetrisch. | + | :** ungeraden Zähler und Nenner besitzt, ist der Graph punktsymmetrisch. |
}} | }} | ||
#<li value="2"> Welche neuen Funktionen erhält mann, wenn man bei den Exponenten der Funktione auch für den Nenner ganze Zahlen statt nur natürliche Zahlen erlaubt, also wenn gilt f(x) = x<sup>p/q</sup> mit <math>p,q \in \mathbb{Z}</math>?</li> | #<li value="2"> Welche neuen Funktionen erhält mann, wenn man bei den Exponenten der Funktione auch für den Nenner ganze Zahlen statt nur natürliche Zahlen erlaubt, also wenn gilt f(x) = x<sup>p/q</sup> mit <math>p,q \in \mathbb{Z}</math>?</li> | ||
Version vom 10. Februar 2009, 17:56 Uhr
Die Graphen der Funktionen mit f(x) = xp/q, p ∈ Z und q ∈ IN
Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen Bruch der Form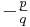 
mit 
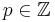und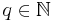 
als Exponenten haben. Man spricht dann von Potenzfunktionen mit gebrochen rationalem Exponenten.
Vergleich mit Funktionen aus vorangegangenen Stufen
|
|
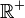eingeschränkt. Bei allen anderen Funktionen ist der Definitionsbereich 
.
?
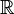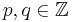