Trigonometrische Funktionen: Unterschied zwischen den Versionen
(Video eingefügt) |
(→Experimentier-Ecke: Video eingefügt) |
||
| Zeile 80: | Zeile 80: | ||
Du hast doch bestimmt einen Zirkel, oder? Genauer gesagt benötigst du nicht den Zirkel, sondern nur die Bleistiftmine für dieses Experiment. Die Mine sollte schräg angefeilt sein. Nimm die Mine aus dem Zirkel und lege sie auf ein Blatt Papier. Wenn du die Mine nun mit einem leichten Druck über das Papier rollst, kannst du den Graphen einer Sinusfunktion erkennen. Diesen kannst du dann gerne noch mit einem Stift nachfahren. | Du hast doch bestimmt einen Zirkel, oder? Genauer gesagt benötigst du nicht den Zirkel, sondern nur die Bleistiftmine für dieses Experiment. Die Mine sollte schräg angefeilt sein. Nimm die Mine aus dem Zirkel und lege sie auf ein Blatt Papier. Wenn du die Mine nun mit einem leichten Druck über das Papier rollst, kannst du den Graphen einer Sinusfunktion erkennen. Diesen kannst du dann gerne noch mit einem Stift nachfahren. | ||
}} | }} | ||
| − | |{{#ev:youtube| | + | |{{#ev:youtube|UfDOp2oE7-k|150}}|| |
---- | ---- | ||
[[zw:Trigonometrische Funktionen]] | [[zw:Trigonometrische Funktionen]] | ||
Version vom 15. Februar 2009, 12:06 Uhr
 |
Hallo! Wäre es nicht toll, wenn du hellsehen könntest? Wenn du den Graphen eines Funktionsterms auch ohne Wertetabelle direkt zeichnen könntest? Wenn du aus dem Graphen einer Funktion deren Term ablesen könntest? Für die linearen und die quadratischen Funktionen beherrschst du diese Kunst wahrscheinlich schon. Dann wirst du vieles von deinem Wissen auf die allgemeine Sinus- und Kosinusfunktion übertragen können. |
|
Hinweise:
|
|
Dieser Lernpfad besteht aus drei Stationen, die du am besten nacheinander bearbeitest. Klicke dazu einfach auf die gewünschte Station! <graphviz> digraph G { rankdir=RL; "Term" -> "Graph"[label=" "]; edge [color = white]; "Term" -> "Hellsehen"; "Hellsehen" -> "Graph"; edge [color = black]; rankdir=LR; "Graph" -> "Term"; } </graphviz>
|
|
Experimentier-Ecke
|
|
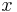 -Achse mit Vielfachen von
-Achse mit Vielfachen von 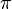 beschriftet. Indem man die
beschriftet. Indem man die 
