Potenzfunktionen - 5. Stufe: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 2: | Zeile 2: | ||
'''[[Potenzfunktionen|Start]] - [[Potenzfunktionen Einführung|Einführung]] - [[Potenzfunktionen 1. Stufe|1. Stufe]] - [[Potenzfunktionen 2. Stufe|2. Stufe]] - [[Potenzfunktionen 3. Stufe|3. Stufe]] - [[Potenzfunktionen 4. Stufe|4. Stufe]] - [[Potenzfunktionen 5. Stufe|5. Stufe]] - [[Potenzfunktionen Test|Test]]'''</div> | '''[[Potenzfunktionen|Start]] - [[Potenzfunktionen Einführung|Einführung]] - [[Potenzfunktionen 1. Stufe|1. Stufe]] - [[Potenzfunktionen 2. Stufe|2. Stufe]] - [[Potenzfunktionen 3. Stufe|3. Stufe]] - [[Potenzfunktionen 4. Stufe|4. Stufe]] - [[Potenzfunktionen 5. Stufe|5. Stufe]] - [[Potenzfunktionen Test|Test]]'''</div> | ||
| − | == Die Graphen der Funktionen mit f(x) = x<sup>p/q</sup>, p <small>∈</small> Z und q <small>∈</small> IN== | + | == *Ergänzung für interessiert Schülerinnen und Schüler:<br>Die Graphen der Funktionen mit f(x) = x<sup>p/q</sup>, p <small>∈</small> Z und q <small>∈</small> IN== |
'''Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen Bruch der Form <math>\textstyle - \frac{p}{q}</math> mit <math>p \in \mathbb{Z}</math> und <math>q \in \mathbb{N}</math> als Exponenten haben.''' Man spricht dann von Potenzfunktionen mit gebrochen rationalem Exponenten. | '''Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen Bruch der Form <math>\textstyle - \frac{p}{q}</math> mit <math>p \in \mathbb{Z}</math> und <math>q \in \mathbb{N}</math> als Exponenten haben.''' Man spricht dann von Potenzfunktionen mit gebrochen rationalem Exponenten. | ||
Version vom 23. Februar 2009, 17:19 Uhr
*Ergänzung für interessiert Schülerinnen und Schüler:
Die Graphen der Funktionen mit f(x) = xp/q, p ∈ Z und q ∈ IN
Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen Bruch der Form 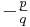 mit
mit 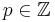 und
und 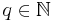 als Exponenten haben. Man spricht dann von Potenzfunktionen mit gebrochen rationalem Exponenten.
als Exponenten haben. Man spricht dann von Potenzfunktionen mit gebrochen rationalem Exponenten.
Vergleich mit Funktionen aus vorangegangenen Stufen
|
Die Graphen der Potenzfunktion mit f(x) = a xp/q
Fasst man alle Variationsmöglichkeiten der Potenzfunktion der vorangegangenen Stufen zusammen, so erhält man die Potenzfunktion 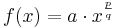 mit den Variablen
mit den Variablen 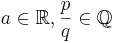 .
.
|
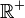 eingeschränkt. Bei allen anderen Funktionen ist der Definitionsbereich
eingeschränkt. Bei allen anderen Funktionen ist der Definitionsbereich 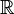 .
.
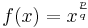 mit
mit 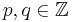 ?
?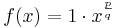 die Veränderung des Graphen, wenn a>1 oder a<0 ist.
die Veränderung des Graphen, wenn a>1 oder a<0 ist.

