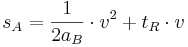|
|
| Zeile 76: |
Zeile 76: |
| | | | |
| | | | |
| − | === Allgemein: f(x) = ax<sup>2 </sup>+ bx=== | + | === f(x) = ax<sup>2 </sup>+ bx=== |
| | | | |
| | {|border="0" Zellspannung="0" cellpadding="4" | | {|border="0" Zellspannung="0" cellpadding="4" |
| − | |valign="top" align = "left" width="450"|Die Funktionen, die wir bis jetzt betrachtet haben sind auch '''quadratische Funktionen''' mit dem Funktionsterm '''ax<sup>2 </sup>+ bx'''. | + | |valign="top" align = "left" width="450"|Die Funktionen, die wir bis jetzt betrachtet haben, sind auch '''quadratische Funktionen'''. Sie haben den Funktionsterm '''ax<sup>2 </sup>+ bx'''. |
| | | | |
| − | Wir wollen nun wie in Aufgabe 3 den Wert für a unverändert lassen und betrachten nur den Parameter '''b'''. | + | Wir lassen nun wie in Aufgabe 3 den '''Wert für a unverändert''' lassen und betrachten nur '''b'''. |
| | <br /> | | <br /> |
| | | | |
| Zeile 87: |
Zeile 87: |
| | NUMMER=4| | | NUMMER=4| |
| | ARBEIT= | | ARBEIT= |
| − | :Untersuche an dem Applet rechts nun den Einfluss von b auf den Verlauf des Graphen. | + | :Untersuche an dem Applet rechts den Einfluss von b auf den Verlauf des Graphen. |
| − | :Was fällt dir auf? | + | :#Was bleibt gleich? |
| − | :Verändere b so, dass....<br /> | + | :#Was ändert sich? |
| − | # ...b ....<br /> | + | |
| − | # ...b...<br />
| + | |
| − | | + | |
| − | :Vergleiche mit dem Graphen der Funktion g mit g(x)=½ x².
| + | |
| | | | |
| | :{{Lösung versteckt|1= | | :{{Lösung versteckt|1= |
| − | # | + | #Die Weite der Parabel bleibt gleich. |
| | + | #Der Scheitel wird verschoben. |
| | }} | | }} |
| | }} | | }} |
| Zeile 105: |
Zeile 102: |
| | ARBEIT= | | ARBEIT= |
| | #Gibt es einen Zusammenhang zwischen dem blauen und grünen Graphen? Experimentiere erneut mit dem ersten Applet und bestätige deine Vermutung. | | #Gibt es einen Zusammenhang zwischen dem blauen und grünen Graphen? Experimentiere erneut mit dem ersten Applet und bestätige deine Vermutung. |
| − | #Setzt den Satz fort: "Wenn zwei Graphen spiegelbildlich bezüglich der y-Achse liegen, dann ... | + | #Setzt den Satz fort: "''Die Graphen liegen spiegelbildlich bezüglich der y-Achse für'' ... |
| | + | |
| | + | :{{Lösung versteckt|1= |
| | + | #Der blaue und der grüne Graph liegen symmetrisch zur y-Achse. |
| | + | #""Die Graphen liegen spiegelbildlich bezüglich der y-Achse für''' b = 2 und b = -2'''. |
| | + | }} |
| | }} | | }} |
| | | | |
Version vom 27. Februar 2009, 22:13 Uhr
Der Anhalteweg
Wir haben oben gesehen, dass man selbst bei relativ moderaten Geschwindigkeiten mit beachtlichen Bremswegen rechnen muss. Dabei blieb jedoch noch unberücksichtigt, dass der Anhalteweg nicht allein der reine Bremsweg ist, sondern dass zum Bremsweg auch noch der sogenannte Reaktionsweg hinzukommt.
Der Bremsweg ist derjenige Weg, den das Fahrzeug vom Beginn des Bremsvorgangs bis zum Stillstand zurücklegt. Er berücksichtigt also nicht, dass man nach dem Auftreten des Hindernisses eine gewisse Zeit (die Reaktionszeit') benötigt, bis man überhaupt reagieren kann und bremst. Der Weg, den das Fahrzeug angesichts der Reaktionszeit noch ungebremst zurücklegt, nennt man Reaktionsweg.
Aufgabe 1 
- Man kann davon ausgehen, dass die Reaktionszeit bei einem gewöhnlichen Autofahrer nicht länger als eine Sekunde ist. Berechne den Reaktionsweg , der sich bei einer Geschwindigkeit von 30 km/h, 50 km/h, 100 km/h aus einer Reaktionszeit von einer Sekunde ergibt.
- Ermittle eine Formel, mit Hilfe derer man den Reaktionsweg aus der Geschwindigkeit berechnen kann. Geh dabei wieder von einer Reaktionszeit von einer Sekunde aus.
- Ermittle eine möglichst einfache Formel, mit Hilfe derer man den Anhalteweg aus der Geschwindigkeit berechnen kann.
- Stelle den Anhalteweg in Abhängigkeit von der Geschwindigkeit grafisch dar. Gehe wieder von einer Reaktionszeit von 1 Sekunde aus.
- [Lösung anzeigen][Lösung ausblenden]
- 1. v = 30 km/h <=> 30 km in einer Stunde <=> 30000 m in 3600 Sekunden <=>
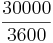 m in 1 Sekunde <=> 8,3 m in einer Sekunde m in 1 Sekunde <=> 8,3 m in einer Sekunde
- D.h. bei einer Geschwindigkeit von 30 km/h und einer Reaktionszeit von 1 Sekunde beträgt der Reaktionsweg ca. 8,3 m.
- genauso folgt: v = 50 km/h => Reaktionsweg ca. 13,9 m und v = 100 km/h => Reaktionsweg ca. 27,8 m
- 2. Reaktionsweg = Geschwindigkeit (in m/s) mal Reaktionszeit
- 3. Anhalteweg = Bremsweg + Reaktionsweg bzw.
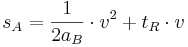
- 4.
|
Experimentieren mit einem Applet zum Anhalteweg
Aufgabe 2 
- Experimentiere mit dem nachfolgenden Applet.
- Beschreibe, welchen Einfluss Geschwindigkeit, Bremsbeschleunigung und Reaktionszeit auf den Anhalteweg haben.
- Bei welchem Wert für a ist der Anhalteweg bei einer Geschwindigkeit von 70 km/h und einer Reationszeit von 1,5 s ungefähr 70 m lang?
- [Lösung anzeigen][Lösung ausblenden]
- 1. ---
- 2. Der Anhalteweg ist umso länger,
- je höher die Geschwindigkeit ist,
- je geringer die Bremsbeschleunigung ist,
- je höher die Reaktionszeit ist.
- 3. a = 4,6 m/s2
|
Im folgenden Applet ist der Zusammenhang zwischen Geschwindigkeit und Anhalteweg dargestellt worden. Mit Hilfe der Schieberegler können Geschwindigkeit v, Bremsbeschleunigung aB und Reaktionszeit tR variiert werden.
Aufgabe 3 
- Es passierte an einem sonnigen Tag, irgendwo auf einer idyllischen Straße durch einen lichten Wald. Herr Meier fuhr in seinem Cabriolet mit entspannten 80 km/h die kerzengerade Straße entlang, als plötzlich 60 m vor ihm ein Hirsch auf die Straße läuft...
- Wie geht die Geschichte aus, wenn Herr Meier
- hochkonzentriert auf den Verkehr geachtet hat (tR = 1,0 s),
- er gerade mit einem Freund telefoniert hat (tR = 2,0 s) ,
- Wie schnell hätte Herr Meier höchstens fahren dürfen, um rechtzeitig zum Stehen zu kommen, obwohl er zwei Bier und einen Verdauungsschnaps zum Mittagessen getrunken hatte (tR = 2,5 s)?
- Verwende jeweils aB = 7 m/s2
- [Lösung anzeigen][Lösung ausblenden]
|
f(x) = ax2 + bx
| Die Funktionen, die wir bis jetzt betrachtet haben, sind auch quadratische Funktionen. Sie haben den Funktionsterm ax2 + bx.
Wir lassen nun wie in Aufgabe 3 den Wert für a unverändert lassen und betrachten nur b.
Aufgabe 4 
- Untersuche an dem Applet rechts den Einfluss von b auf den Verlauf des Graphen.
- Was bleibt gleich?
- Was ändert sich?
- [Lösung anzeigen][Lösung ausblenden]
- Die Weite der Parabel bleibt gleich.
- Der Scheitel wird verschoben.
|
Aufgabe 5 
- Gibt es einen Zusammenhang zwischen dem blauen und grünen Graphen? Experimentiere erneut mit dem ersten Applet und bestätige deine Vermutung.
- Setzt den Satz fort: "Die Graphen liegen spiegelbildlich bezüglich der y-Achse für ...
- [Lösung anzeigen][Lösung ausblenden]
- Der blaue und der grüne Graph liegen symmetrisch zur y-Achse.
- ""Die Graphen liegen spiegelbildlich bezüglich der y-Achse für b = 2 und b = -2.
|
|
|
Das Applet zeigt den Graphen einer Funktion f mit f(x) = ½ x²+bx. Hierbei steht b für eine beliebige reelle Zahl
Mit Hilfe des Schiebereglers (unten links im Applet) kannst du den Wert für b variieren.
|

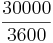 m in 1 Sekunde <=> 8,3 m in einer Sekunde
m in 1 Sekunde <=> 8,3 m in einer Sekunde