Zugang zur Poissonverteilung: Unterschied zwischen den Versionen
(→Die Poissonverteilung) |
|||
| Zeile 227: | Zeile 227: | ||
; Poisson-Verteilung | ; Poisson-Verteilung | ||
| − | {{Merksatz|MERK= Wahrscheinlichkeitsfunktionen mit einer grafischen Darstellung wie jener des Autofahrerbeispiels, wurden nach dem französischen Mathematiker Simeón Denis Poisson (1781–1840) benannt und treten bei sehr seltenen Ereignissen und einer großen Stichprobe auf. Poisson hat erkannt, dass der Verlauf der relativen Häufigkeiten eine Form hat, die an den Graphen folgender Funktion erinnert:<br /><math>f(x)={{e^{{-p\cdot n}}}\cdot (p\cdot n)^x \over x!}</math> , wobei p die Wahrscheinlichkeit darstellt, mit welcher das Ereignis eintritt; n ist die Anzahl der Stichprobengröße.}} | + | {{Merksatz|MERK= Wahrscheinlichkeitsfunktionen mit einer grafischen Darstellung wie jener des Autofahrerbeispiels, wurden nach dem französischen Mathematiker Simeón Denis Poisson (1781–1840) benannt und treten bei sehr seltenen Ereignissen und einer großen Stichprobe auf. Poisson hat erkannt, dass der Verlauf der relativen Häufigkeiten eine Form hat, die an den Graphen folgender Funktion erinnert:<br /><math>f(x)={{e^{{-p\cdot n}}}\cdot (p\cdot n)^x \over x!}</math> , wobei p die Wahrscheinlichkeit darstellt, mit welcher das Ereignis eintritt; n ist die Anzahl der Stichprobengröße. Man spricht bei einer stetigen Funktion dieser Form von einer "Trägerkurve" als Annäherung der diskreten Wahrscheinlichkeitsfunktion.}} |
---- | ---- | ||
{{Arbeiten|NUMMER=| | {{Arbeiten|NUMMER=| | ||
| − | ARBEIT=Finde durch Probieren mit Hilfe des GeoGebra-Applets eine | + | ARBEIT=Finde durch Probieren mit Hilfe des GeoGebra-Applets eine Funktion der oben erwähnten Form, die der Wahrscheinlichkeitsfunktion der Autounfälle möglichst nahe kommt. Variiere dabei die Parameter p und n durch Einsetzen der Schieberegler.}} |
| Zeile 238: | Zeile 238: | ||
<ggb_applet height="400" width="800" filename="Poisson_1.ggb" /> | <ggb_applet height="400" width="800" filename="Poisson_1.ggb" /> | ||
---- | ---- | ||
| − | |||
= Der Begriff der Verteilungsfunktion= | = Der Begriff der Verteilungsfunktion= | ||
Version vom 30. März 2009, 13:12 Uhr
Heidi Metzger-Schuhäker, Peter Hofbauer, Gabi Bleier
Inhaltsverzeichnis |
Es gibt nur gute Autofahrer, oder?
Die Behauptung
Die meisten Autofahrer behaupten von sich, dass ihre Fahrkünste nicht schlechter als durchschnittlich sind. Ist das möglich oder handelt es sich um Selbstüberschätzung? Wie kann man die Fahrkünste überhaupt bewerten? Als Maß der Sicherheit soll die Anzahl der Unfälle gelten, in die ein(e) Fahrer(in) im Laufe des Lebens verwickelt ist.
Statistische Auswertung
Da als Maß der Sicherheit die Anzahl der Unfälle gilt, in die ein(e) Fahrer(in) im Laufe des Lebens verwickelt ist, legen wir unserer Analyse eine Unfallstatistik zugrunde. Du kannst den Zusammenhang selbst untersuchen. Hier sind die Daten, die die Polizei gesammelt hat: Stichprobe: 100 Fahrer
| Anzahl der Unfälle | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Personen | 6 | 17 | 23 | 20 | 14 | 9 | 4 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
|
Lösung:
Mittelwert: 3,22
Standardabweichung: 7,34
Anzahl der Autofahrer mit höchstens 3 Unfällen: 66 von 100, also 66%.
Der Begriff der Wahrscheinlichkeitsfunktion
Als erstes Modell könntest du als Beurteilung der Sicherheit eines Autofahrers bzw. einer Autofahrerin die Anzahl der Unfälle, in welche die Person im Laufe ihres Lebens verwickelt war, heranziehen.
Die Zufallsvariable
- Zufallsvariable
|
Merke:
Eine Zufallsvariable X ordnet jedem Ergebnis eines Zufallsexperimentes verschiedenene, nicht vorhersagbare Zahlen x zu. |
In diesem Beispiel ist die Zufallsvariable X das Maß der Sicherheit eines Autofahrers, es werden hier entsprechend die Anzahlen der Unfälle, also die Zahlen 0 bis 20 zugeordnet.
- diskrete Zufallsvariable
|
Merke:
Wenn dabei die zugeordneten Werte abzählbar sind, also einem Zählprozess zugrunde liegen, spricht man von diskreten Zufallsvariablen. |
|
Finde eigenständig weitere Beispiele für diskrete Zufallsvariable! |
Wir wollen nun versuchen, aus der vorliegenden Stichprobe der Polizei etwas allgemeinere Aussagen treffen zu können. Da es sich um eine Stichprobe mittlerer Größe handelt, ist es sinnvoll, sich die relativen Häufigkeiten genauer anzusehen.
|
| Zufallsvariable (Anzahl der Unfälle) X=x | x=0 | x=1 | x=2 | x=3 | x=4 | x=5 | x=6 | x=7 | x=8 | x=9 | x=10 | x=11 | x=12 | x=13 | x=14 | x=15 | x=16 | x=17 | x=18 | x=19 | x=20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| relative Häufigkeiten | 0.06 | 0,17 | 0,23 | 0,20 |
Lösung zu 1:
Approximation der (statistischen) Wahrscheinlichkeit mit Hilfe von relativen Häufigkeiten:
Nähern sich bei wachsendem Stichprobenumfang die relativen Häufigkeiten des Eintretens eines Ereignisses E einer bestimmten Zahl p(E) so bezeichnet man p(E) als Wahrscheinlichkeit für das Eintreten des Ereignises E. Man schreibt 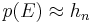 für sehr großes n.
für sehr großes n.
Lösung zu 2:
Die Darstellung mittels relativer Häufigkeiten
- Wahrscheinlichkeitsfunktion einer diskreten Zufallsvariable
|
Merke:
Unter einer Wahrscheinlichkeitsfunktion f der diskreten Zufallsvariablen X versteht man die Funktion, die den Funktionswerten von X, also den zugeordneten Werten x die Wahrscheinlichkeit p ihres Eintretens zuordnet. |
In diesem Beispiel entspricht die grafische Darstellung der relativen Häufigkeiten also einer Wahrscheinlichkeitsfunktion.
|
Beschreibe den Verlauf der Funktionswerte. Macht es Sinn, die einzelnen Werte miteinander zu verbinden? |
Lösung:
Wenn man die Darstellung der relativen Häufigkeiten betrachtet, so zeigt sich eine deutlich asymmetrische Verteilung. Bei einer zufällig aus der Stichprobe gewählten Person ist der berechnete Mittelwert von 3 Unfällen eine optimale Prognose, der Erwartungswert. Aus der Graphik zeigt sich, dass die meisten Personen eher in wenige Unfälle verwickelt sind. Größere Unfallanzahlen treten hingegen viel seltener auf.
Da Unfälle nur ganzzahlige auftreten können (du kannst nicht 0,3 Unfälle haben) ist es nicht sinnvoll, die einzelnen Werte zu verbinden. Die Wahrscheinlichkeitsfunktion ist deshalb nur für ganzzahlige nicht negative Werte definiert.Die Poissonverteilung
- Poisson-Verteilung
|
Merke:
Wahrscheinlichkeitsfunktionen mit einer grafischen Darstellung wie jener des Autofahrerbeispiels, wurden nach dem französischen Mathematiker Simeón Denis Poisson (1781–1840) benannt und treten bei sehr seltenen Ereignissen und einer großen Stichprobe auf. Poisson hat erkannt, dass der Verlauf der relativen Häufigkeiten eine Form hat, die an den Graphen folgender Funktion erinnert: |
|
Finde durch Probieren mit Hilfe des GeoGebra-Applets eine Funktion der oben erwähnten Form, die der Wahrscheinlichkeitsfunktion der Autounfälle möglichst nahe kommt. Variiere dabei die Parameter p und n durch Einsetzen der Schieberegler. |
Der Begriff der Verteilungsfunktion
In der ursprünglichen Aufgabenstellung interessiert uns nicht die Wahrscheinlichkeit, mit welcher ein Autofahrer im Laufe seines Lebens eine bestimmte Anzahl von Unfällen hat. Vielmehr interessiert uns die Wahrscheinlichkeit, mit welcher Zufallsvariable Werte annehmen, die nicht größer als ein fest vorgegebener Wert sind, also ein Autofahrer nicht mehr als vier Unfälle im Laufe seines Lebens hat.
|
Lösung zu 1:
Lösung zu 2:
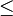 höchste Anzahl ist ein sicheres Ereignis und liegt bei 100% bzw. 1.
höchste Anzahl ist ein sicheres Ereignis und liegt bei 100% bzw. 1.Lösung zu 3:
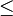 3)=P(X=0)+P(X=1)+P(X=2)+P(X=3)=66%; POISSONVERTEILUNG: zB. bei n=4500, p=0,00062: 69%
3)=P(X=0)+P(X=1)+P(X=2)+P(X=3)=66%; POISSONVERTEILUNG: zB. bei n=4500, p=0,00062: 69%Lösung zu 4:
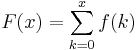
Da es bei dieser Darstellung Sprungstellen bei den jeweils ganzzahligen Werten gibt, handelt es sich bei der grafischen Darstellung solcher Verteilungsfunktionen um Treppenfunktionen.
Weitere Aufgaben
Zum Schluss noch weitere Aufgaben, um die neuerlernte Poissonverteilung selbständig anzuwenden:
|
Ein deutscher Statistiker namens Bortkiewicz führte zu Beginn des 20. Jahrhunderts eine versicherungsmathematisch interessante Untersuchung durch:
Zu wie vielen tödlichen Unfällen durch Pferdehufschlag kam es in der preußischen Armee?
Die folgende Tabelle enthält die Statistik der Unfallopfer von 10 Kavallerieregimentern für einen Zeitraum von 20 Jahren (dies entspricht 200 "Regimentsjahren"). Berechne das arithmetische Mittel und setzte diese Zahl als Parameter |
| Zahl der Todesopfer | 0 | 1 | 2 | 3 | 4 | >4 |
|---|---|---|---|---|---|---|
| Zahl der Regimentsjahre | 109 | 65 | 22 | 3 | 1 | 0 |
|
Die mittlere Ankunftsrate der Bestellungen per E-Mail auf unserem Server beträgt |
|
Die Häufigkeit von Kreditausfällen kann näherungsweise durch eine POISSON-Verteilung dargestellt werden. Wie groß ist für ein Portfolio von z.B. n=1000 Krediten mit einer einheitlichen und unabhängigen Ausfallwahrscheinlichkeit von p=1% die Wahrscheinlichkeit, dass es – etwa innerhalb eines Jahres – zu mehr als 2 Ausfällen kommt. |
|
Dieser Lernpfad wurde erstellt von:
Peter Hofbauer, Heidi Metzger-Schuhäker, Gabi Bleier |

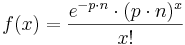 , wobei p die Wahrscheinlichkeit darstellt, mit welcher das Ereignis eintritt; n ist die Anzahl der Stichprobengröße. Man spricht bei einer stetigen Funktion dieser Form von einer "Trägerkurve" als Annäherung der diskreten Wahrscheinlichkeitsfunktion.
, wobei p die Wahrscheinlichkeit darstellt, mit welcher das Ereignis eintritt; n ist die Anzahl der Stichprobengröße. Man spricht bei einer stetigen Funktion dieser Form von einer "Trägerkurve" als Annäherung der diskreten Wahrscheinlichkeitsfunktion.
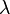 ein´. (Erwartungswert
ein´. (Erwartungswert 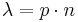 ). Vergleiche mit Hilfe einer Tabelle die Werte der relativen Häufigkeiten und der possionverteilten Wahrscheinlichkeitsfunktion!
). Vergleiche mit Hilfe einer Tabelle die Werte der relativen Häufigkeiten und der possionverteilten Wahrscheinlichkeitsfunktion!
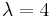 pro Tag.
Wie groß ist die Wahrscheinlichkeit, dass mehr als 8 Bestellungen pro Tag hereinkommen.
pro Tag.
Wie groß ist die Wahrscheinlichkeit, dass mehr als 8 Bestellungen pro Tag hereinkommen.


