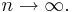Potenzfunktionen - 1. Stufe: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(Lösung zu Aufgabe 5 bearb.) |
(Lösung zu Aufgabe 5: Layout) |
||
| Zeile 108: | Zeile 108: | ||
# Bestimme a und n so, dass der Graph durch die Punkte '''A(-1;-1)''' und '''B(0,5;3)''' verläuft. Was fällt auf? Erkläre deine Beobachtungen. | # Bestimme a und n so, dass der Graph durch die Punkte '''A(-1;-1)''' und '''B(0,5;3)''' verläuft. Was fällt auf? Erkläre deine Beobachtungen. | ||
<br /> | <br /> | ||
| − | zu 1.) Lösung: a=-0,5 und n=3. Begründung: An der Stelle <math>x=1</math> ist <math>f(1)=(-0,\!5)\cdot 1^3 = -0,\!5</math> <br /> | + | {{ Lösung versteckt | |
| − | und an der Stelle <math>x=-2</math> ist <math>f(-2)=(-0,\!5)\cdot (-2)^3 = (-0,\!5)\cdot(-8)=4</math> <br /> | + | :zu 1.) Lösung: <math>a=-0,5</math> und <math>n=3.</math> <br /> |
| − | zu 2.) Es gibt keine Lösung! <br /> | + | : '''Begründung:''' An der Stelle <math>x=1</math> ist <math>f(1)=(-0,\!5)\cdot 1^3 = -0,\!5</math> <br /> |
| − | : | + | :: und an der Stelle <math>x=-2</math> ist <math>f(-2)=(-0,\!5)\cdot (-2)^3 = (-0,\!5)\cdot(-8)=4</math> <br /> |
| + | :zu 2.) Es gibt keine Lösung! <br /> | ||
| + | : '''Begründung:''' <br /> | ||
::* Die y-Komponente des Punktes A(-1;-1) ist negativ, die des Punktes B(0,5;3) positiv. Also sucht man eine Potenzfunktion <math>f(x)=a\cdot x^n</math> mit ungeradem <math>n</math> (vgl. Aufgabe 2), die monoton steigt. <br /> | ::* Die y-Komponente des Punktes A(-1;-1) ist negativ, die des Punktes B(0,5;3) positiv. Also sucht man eine Potenzfunktion <math>f(x)=a\cdot x^n</math> mit ungeradem <math>n</math> (vgl. Aufgabe 2), die monoton steigt. <br /> | ||
::* Damit der Funktionsgraph durch A(-1;-1) läuft, muss darin der Parameter <math>a=1</math> sein (vgl. Aufgabe 4). <br /> | ::* Damit der Funktionsgraph durch A(-1;-1) läuft, muss darin der Parameter <math>a=1</math> sein (vgl. Aufgabe 4). <br /> | ||
::* Damit der Funktionsgraph durch B(0,5;3) läuft, muss <math>f(0,\!5)=a\cdot (0,\!5)^n=3</math> gelten. <br /> | ::* Damit der Funktionsgraph durch B(0,5;3) läuft, muss <math>f(0,\!5)=a\cdot (0,\!5)^n=3</math> gelten. <br /> | ||
:: Zusammengenommen sucht man also nach einer natürlichen Zahl n, die <math>(0,\!5)^n=3</math> erfüllt. Diese kann nicht exisitieren, da <math>(0,\!5)^n \to 1</math> für <math>n \to \infty.</math> | :: Zusammengenommen sucht man also nach einer natürlichen Zahl n, die <math>(0,\!5)^n=3</math> erfüllt. Diese kann nicht exisitieren, da <math>(0,\!5)^n \to 1</math> für <math>n \to \infty.</math> | ||
| + | }} | ||
}} | }} | ||
|} | |} | ||
Version vom 31. März 2009, 13:00 Uhr
Inhaltsverzeichnis |
Die Graphen der Funktionen mit f(x) = xn, n ∈ IN
Gerade Potenzen
Wir betrachten zunächst die Graphen der Funktionen mit f(x) = xn, wenn n eine gerade Zahl ist, also n = 2, 4, 6, ...
|
Ungerade Potenzen
Wir betrachten nun die Graphen der Funktionen mit 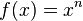 , wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..
, wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..
|
Teste dein Wissen
|
Wir betrachten die Funktionen mit f(x) = xn, n eine natürliche Zahl
|
Die Graphen von f(x) = a xn, mit a ∈ IR
Wir betrachten jetzt die Funktionen mit 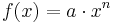 , wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n ∈ IN, a ∈ IR .
, wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n ∈ IN, a ∈ IR .
|
|
Teste Dein Wissen

|
Als nächstes erfährst du etwas über Potenzfunktionen mit negativen ganzzahligen Exponenten. |
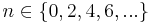 . Dann gilt:
. Dann gilt:
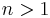 sind alle Graphen im Intervall ]-∞,0[ streng monoton fallend, im Intervall ]0,∞[ streng monoton steigend; die Graphen verlaufen durch den Ursprung (0;0) und 0 ist der kleinste Funktionswert. Ein größter Funktionswert wird nicht angenommen.
sind alle Graphen im Intervall ]-∞,0[ streng monoton fallend, im Intervall ]0,∞[ streng monoton steigend; die Graphen verlaufen durch den Ursprung (0;0) und 0 ist der kleinste Funktionswert. Ein größter Funktionswert wird nicht angenommen.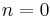 gilt
gilt 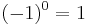 nach Defition der Potenzen. Alle anderen Exponenten
nach Defition der Potenzen. Alle anderen Exponenten 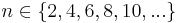 sind Vielfache von 2, also von der Art
sind Vielfache von 2, also von der Art 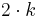 für alle
für alle 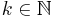 ; dann gilt:
; dann gilt: 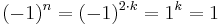 für alle
für alle 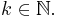
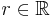 ist
ist 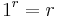 und damit insbesondere für
und damit insbesondere für 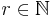 .
.
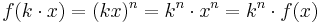 .
.
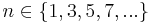 . Dann gilt:
. Dann gilt:
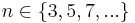 haben die Funktionen im Ursprung einen Terassen- bzw. Sattelpunkt, sind dort also nicht streng-monoton steigend.
haben die Funktionen im Ursprung einen Terassen- bzw. Sattelpunkt, sind dort also nicht streng-monoton steigend.
 , alle Werte werden durchlaufen (die Funktion ist damit surjektiv).
, alle Werte werden durchlaufen (die Funktion ist damit surjektiv).
 in allen Graphen.
in allen Graphen.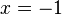 ist
ist 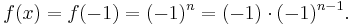 Da
Da 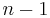 eine gerade Zahl. Deswegen gilt weiter:
eine gerade Zahl. Deswegen gilt weiter: 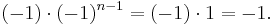
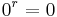 und
und 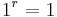 für alle
für alle 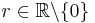 .
.
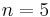 durchlaufen:
durchlaufen: 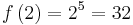 .
.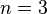 durchlaufen:
durchlaufen: 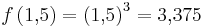 .
.
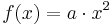 . Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
. Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
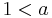 wird der Graph der Funktion gestreckt und wird für
wird der Graph der Funktion gestreckt und wird für 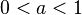 gestaucht.
gestaucht.
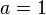 bleibt er unverändert
bleibt er unverändert
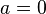 wird die Funktion zur Nullfunktion mit
wird die Funktion zur Nullfunktion mit 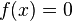 für alle
für alle  .
.
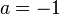 bewirkt eine Spiegelung des Graphen an der x-Achse; alle übrigen Fälle ergeben sich daraus.
bewirkt eine Spiegelung des Graphen an der x-Achse; alle übrigen Fälle ergeben sich daraus.
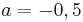 und
und 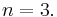
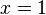 ist
ist 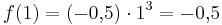
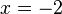 ist
ist 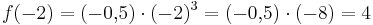
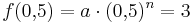 gelten.
gelten. 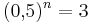 erfüllt. Diese kann nicht exisitieren, da
erfüllt. Diese kann nicht exisitieren, da 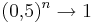 für
für