Potenzfunktionen - 3. Stufe: Unterschied zwischen den Versionen
K (Verlinkung Stufe 4 eingef.) |
K (hat „Potenzfunktionen 3. Stufe“ nach „Potenzfunktionen/ 3. Stufe“ verschoben: Unterseite) |
Version vom 3. Januar 2011, 22:54 Uhr
Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen (positiven) Stammbruch der Form 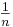 mit
mit 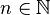 als Exponenten haben.
als Exponenten haben.
Inhaltsverzeichnis |
Die Graphen der Funktionen mit f(x) = x1/n, n ∈ IN
Funktionsgraph kennenlernen
|
Vergleich mit Funktionen aus Stufe 2
|
Bezeichungen: Potenzen und Wurzeln
Wir betrachten hier Potenzfunktionen mit 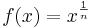 ,
, 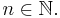
|
Merke:
Wegen Im Falle Im Falle |
Den Grund für diese Bezeichnungen zeigen die folgenden Beispiele:
Beispiel: Quadratwurzeln
|
Beispielsweise ergibt sich die Länge der Diagonale Die Lösung ist |
|
Auch die Länge der Raumdiagonale 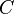 im Einheitswürfel (das ist ein Würfel mit der Kantenlänge a=1) ergibt sich über eine analoge Rechnung aus dem Satz des Satz des Pythagoras (hier: im Einheitswürfel (das ist ein Würfel mit der Kantenlänge a=1) ergibt sich über eine analoge Rechnung aus dem Satz des Satz des Pythagoras (hier: 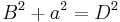 ) zu: ) zu:
Die Lösung ist also |
Beispiel: Kubikwurzel
Das Volumen 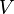 eines Würfels (lat.: "cubus") der Kantenlänge
eines Würfels (lat.: "cubus") der Kantenlänge 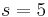 ergibt sich über:
ergibt sich über:
Umgekehrt erhält man die Kantenlänge eines Würfels mit Volumen 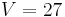 durch ziehen der 3.-Wurzel:
durch ziehen der 3.-Wurzel:
Einfluss von Parametern
|
In nebenstehendem Applet kannst Du die Parameter
|
*Zum Weiterdenken: Definitionsbereich der Wurzelfunktionen
(*Zusatzinformation, freilwillige Ergänzung)
Einschränkung auf IR+0
Gelegentlich findet man in Büchern oder auch im Internet folgende Darstellung: ![\sqrt[3]{-8}= -2,](/images/math/5/b/6/5b6fa0df280fc90fa5e52cf58c8949fc.png)
Wegen
erscheint das richtig zu sein, allerdings kann diese Festlegung zu Widersprüchen führen, wie das folgende Beispiel zeigt:
Um solche Fälle von Nicht-Eindeutigkeiten, aber auch um Fallunterscheidungen bei 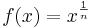 für gerade und ungerade n zu vermeiden, schränkt man den Definitionsbereich ID der Wurzelfunktionen grundsätzlich auf die nicht-negativen reellen Zahlen ein, also:
für gerade und ungerade n zu vermeiden, schränkt man den Definitionsbereich ID der Wurzelfunktionen grundsätzlich auf die nicht-negativen reellen Zahlen ein, also:
![f(x) = \sqrt[n]{x}](/images/math/8/4/5/845e92e8d6fb632e22343997822d31e4.png) mit
mit 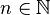 und
und 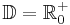
Wurzelfunktion auf ganz IR
Will man eine Wurzelfunktion g dennoch auf ganz IR definieren (d.h. ID = IR), dann muss man sie - nach obiger Vorüberlegung - aus zwei einzelnen Wurzelfunktionen zusammensetzen. Man definiere etwa g derart, dass
![g(x):=\begin{cases}\sqrt[n]{x}, &x\geq 0 \\ -\sqrt[n]{-x}, &x<0\end{cases}](/images/math/a/3/a/a3ab5cc5c79181de2e4fb2b10a3c1493.png) .
.
Dann gilt: IDg = IR.

|
Als nächstes erfährst du etwas über Potenzfunktionen, die auch negative Stammbrüchen im Exponenten haben. |
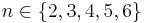 .
.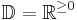 . Der kleinste Funktionswert
. Der kleinste Funktionswert 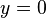 wird für
wird für  angenommen; von da aus steigen die blauen Graphen streng monoton über alle Grenzen an.
angenommen; von da aus steigen die blauen Graphen streng monoton über alle Grenzen an.
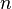 in allen Graphen. Begründung: Es gilt
in allen Graphen. Begründung: Es gilt 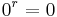 und
und 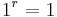 für alle
für alle 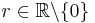 .
.
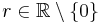 .
.
![x^{\frac{1}{n}}:=\sqrt[n]{x}](/images/math/4/9/9/4999dd3cabd40b13e2c72e4dd52f4963.png) nennt man diese Funktionen auch Wurzelfunktionen. Ihr Definitionsbereich ist (wie die Aufgaben 1 und 2 gezeigt haben)
nennt man diese Funktionen auch Wurzelfunktionen. Ihr Definitionsbereich ist (wie die Aufgaben 1 und 2 gezeigt haben)  mit
mit 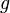 der Bauart
der Bauart 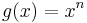 und
und 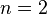 nennt man die Wurzel "Quadratwurzel" und man schreibt:
nennt man die Wurzel "Quadratwurzel" und man schreibt:
![x^{\frac{1}{2}} = \sqrt[2]{x} =: \sqrt{x}](/images/math/0/a/c/0ac01087183dbfa345a1f18b06682aeb.png)
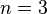 nennt man die Wurzel "Kubikwurzel", i. Z.:
nennt man die Wurzel "Kubikwurzel", i. Z.: 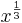 bzw.
bzw. ![\sqrt[3]{x}](/images/math/a/1/0/a10c7f2aa138b1565920d17c22062a35.png) .
.
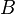 in einem Quadrat der Seitenlänge
in einem Quadrat der Seitenlänge 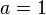 über den Satz des Pythagoras
über den Satz des Pythagoras 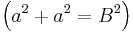 zu:
zu:
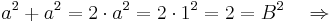
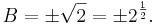
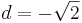 ergibt hier keinen Sinn, da wir nur Längen in der realen Welt betrachten.
ergibt hier keinen Sinn, da wir nur Längen in der realen Welt betrachten.
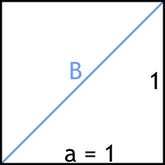
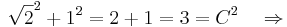
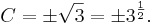
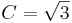 angeben.
angeben.
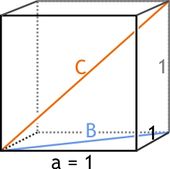
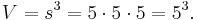
![\sqrt[3]{27}=\sqrt[3]{3\cdot 3 \cdot 3} = \sqrt[3]{3^3} = \sqrt[3]{3}^3 = 3.](/images/math/6/c/c/6cc6c328ea65f968fd01a636602ec89d.png)
 und
und  mit den Schiebereglern verändern.
mit den Schiebereglern verändern.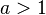 eine Streckung des Graphen in y-Richtung, für
eine Streckung des Graphen in y-Richtung, für 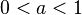 eine Stauchung in y-Richtung; für
eine Stauchung in y-Richtung; für 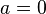 erhält man eine konstante Funktion mit
erhält man eine konstante Funktion mit 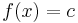 . Wird
. Wird 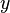 der Wert
der Wert 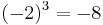
![-2 = \sqrt[3]{-8} = (-8)^{\frac{1}{3}} = (-8)^{\frac{2}{6}} = \left( (-8)^2 \right)^{\frac{1}{6}} = \left( (8)^2 \right)^{\frac{1}{6}} = (8)^{\frac{2}{6}} = (8)^{\frac{1}{3}} = \sqrt[3]{8} = 2.](/images/math/6/1/6/6165c6f8f1d60ceda3379d42bb03efe8.png)

