Quadratische Funktionen Station12: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „<center><span style="background:#FFFACD">Falls es Probleme mit der Ansicht gibt, bitte Firefox als Browser verwenden!</span></center> ==Übungen …“) |
|||
| Zeile 1: | Zeile 1: | ||
<center><span style="background:#FFFACD">Falls es Probleme mit der Ansicht gibt, bitte [[:zw:Firefox|Firefox]] als Browser verwenden!</span></center> | <center><span style="background:#FFFACD">Falls es Probleme mit der Ansicht gibt, bitte [[:zw:Firefox|Firefox]] als Browser verwenden!</span></center> | ||
| − | ==Übungen | + | ==Übungen 3== |
{| | {| | ||
Aktuelle Version vom 12. Mai 2011, 22:15 Uhr
Übungen 3
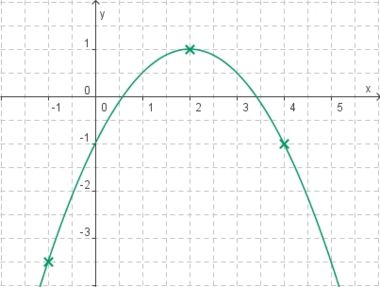
Aufgabe 1: Funktionsterm finden
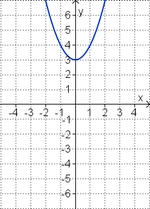
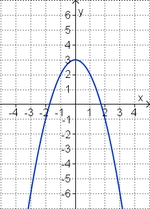
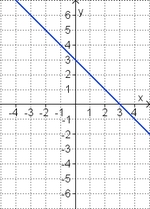
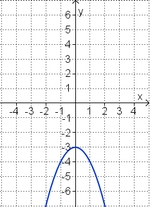
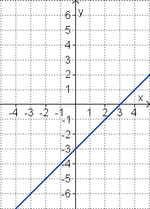
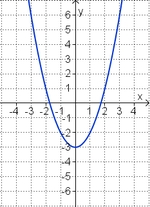
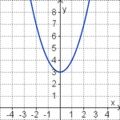
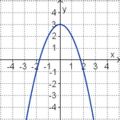
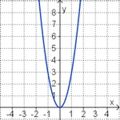
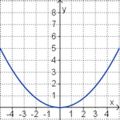
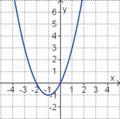
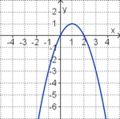
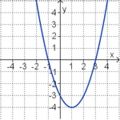
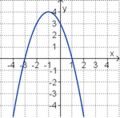
Aufgabe 2: Term und Graph zuordnen Ordne den Funktionsgraphen den richtigen Term zu.
x2 + 3-x2 + 3x - 3-x + 3x2 - 3-x2 - 3
Aufgabe 3: Multiple Choice Kreuze jeweils alle richtigen Aussagen an. f(x) = –2x2 + 3x – 4
Aufgabe 4: Memo-Quiz Finde die richtigen Paare - je ein Funktionsterm und ein Funktionsgraph gehören zusammen. Achte auf die wesentlichen Eigenschaften der Funktion (Öffnung der Parabel, Lage des Scheitels, Nullstellen).
|
