Radioaktiver Zerfall - analytische Herleitung: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(Die Seite wurde neu angelegt: „Die Gleichung <math>N(t)=N_{0} \cdot e^{-\lambda \cdot t}</math> ist eine der bekanntesten der Mathematik und wird in der zehnten Schulstufe eingeführt. In der z…“) |
|||
| Zeile 4: | Zeile 4: | ||
Zusätzlich sind drei Standardaufgaben angegeben, um die Verwendung der Gleichung zu wiederholen. | Zusätzlich sind drei Standardaufgaben angegeben, um die Verwendung der Gleichung zu wiederholen. | ||
| − | [[Diskret-kontinuierlich ]] | + | [[Diskret - kontinuierlich|Zurück zum Lernpfad]] |
Version vom 22. August 2011, 11:37 Uhr
Die Gleichung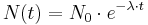 
ist eine der bekanntesten der Mathematik und wird in der zehnten Schulstufe eingeführt. In der zwölften Schulstufe ist es nun mit Hilfe der Integralrechung möglich, ausgehend vom Ansatz 
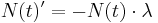obige Relation per Differentialgleichung analytisch herzuleiten.
Unter Rad_zerfall_analytisch.pdf ist diese Herleitung Schritt für Schritt nachvollziehbar. Zuerst wird der allgemeine Fall besprochen und dann der Bezug auf die Anwendung beim radioaktiven Zerfall hergestellt.
Zusätzlich sind drei Standardaufgaben angegeben, um die Verwendung der Gleichung zu wiederholen.
