Trigonometrische Funktionen: Unterschied zwischen den Versionen
K (→Der Biorhythmus) |
K (→(ab hier wird noch gelöscht)) |
||
| Zeile 206: | Zeile 206: | ||
[[zw:Trigonometrische Funktionen]] | [[zw:Trigonometrische Funktionen]] | ||
| − | === ( | + | === (Diese Aufgaben werden evtl. noch gelöscht.)=== |
#[http://www.brichzin.de/unterricht/trigonometr_fkt/trigonometr5.html Hier] kannst beide Parameter c und d von sin(x+c)+d durch Verschieben des Graphen ändern und die Auswirkung auf den Funktionsterm betrachten. Übertrage deine Ergebnisse auf cos(x+c)+d. | #[http://www.brichzin.de/unterricht/trigonometr_fkt/trigonometr5.html Hier] kannst beide Parameter c und d von sin(x+c)+d durch Verschieben des Graphen ändern und die Auswirkung auf den Funktionsterm betrachten. Übertrage deine Ergebnisse auf cos(x+c)+d. | ||
Version vom 8. November 2008, 02:47 Uhr
| Beschreibung |
Es fehlt noch eine Beschreibung des Inhalts der Datei (Was zeigt die Datei?). Bitte diese Information noch nachtragen.
|
|---|---|
| Quelle |
Es fehlt noch die Quelle für die Datei (Woher hat der Uploader die Datei?). Bitte diese Information noch nachtragen.
|
| Urheber bzw. Nutzungsrechtinhaber |
Es fehlt noch der Urheber bzw. der Nutzungsrechteinhaber für die Datei (Wer hat die Datei ursprünglich erstellt?). Bitte diese Information noch nachtragen.
|
Inhaltsverzeichnis |
Hallo!
| Wäre es nicht toll, wenn du hellsehen könntest? Wenn du den Graphen eines Funktionsterms auch ohne Wertetabelle direkt zeichnen könntest? Wenn du aus dem Graphen einer Funktion deren Term ablesen könntest?
Für die linearen und die quadratischen Funktionen beherrscht du diese Kunst wahrscheinlich schon. Dann wirst du vieles von Deinem Wissen auf die allgemeine Sinus- und Cosinusfunktion übertragen können. Viel Spass! |
(dies ist nur ein Test) |
Der Biorhythmus
Mit der Geburt beginnen beim Menschen aktive und passive Phasen, die den körperlichen, seelischen und geistigen Bereich betreffen. Sie treten zyklisch immer wiederkehrend auf. Diese Zyklen heißen Biorhythmen. Wir wollen nun untersuchen, wie man solch unterschiedliche Graphen mathematisch mit Hilfe von Parametern darstellen kann.
Einfluss der Parameter bei der allgemeinen Sinus- und Kosinusfunktion
Wiederholung:
Hefteintrag: Am besten verwendest du hierfür dein Heft im Querformat. Formuliere eine Überschrift und übernehme alle mit gelb hinterlegten Texte. Natürlich darfst du dir aber auch noch zusätzlich Notizen machen.
|
Merke:
Die allgemeine Sinusfunktion lautet
Entsprechend lautet die allgemeine Kosinusfunktion
Dabei sind |
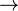 Hinweis: Bei den GeoGebra-Applets ist die
Hinweis: Bei den GeoGebra-Applets ist die 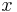 -Achse mit Vielfachen von
-Achse mit Vielfachen von 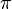 beschriftet. Indem man die
beschriftet. Indem man die 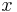 -Achse mit der rechten Maustaste anklickt und "Eigenschaften" wählt, kann man auf die Einheit cm umstellen.
-Achse mit der rechten Maustaste anklickt und "Eigenschaften" wählt, kann man auf die Einheit cm umstellen.
Arbeiten in Expertenteams
Einfluss von 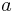 |
Einfluss von 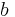 |
Einfluss von  |
Einfluss von 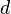
|
|---|---|---|---|
|
Untersuche hier den Einfluss von auf den Graph der Funktion
|
Untersuche hier den Einfluss von auf den Graph der Funktion
|
Untersuche hier den Einfluss von auf den Graph der Funktion
|
Untersuche hier den Einfluss von auf den Graph der Funktion
|
Arbeiten in Expertenteams
Du hast nun eine Menge über den Einfluss der einzelnen Parameter auf das Aussehen der Graphen heraus gefunden. Natürlich können aber die Parameter nicht nur einzeln variiert werden, sondern auch mehrere oder alle gleichzeitig.
Sinus und Kosinus
|
Wie hängen die Sinus- und die Kosinusfunktion zusammen? Erstelle die Graphen
der Funktionen |
Lösung:
Ja genau, die Graphen der beiden Funktionen sind identisch. Genauer gesagt:
|
Merke:
Man erhält den Graphen der Kosinusfunktion indem man den Graphen der Sinusfunktion um Deshalb verhält sich die allgemeine Kosinusfunktion bei Variation ihrer Parameter genauso wie die allgemeine Sinusfunktion. |
Jetzt noch was zum Knobeln!!!
|
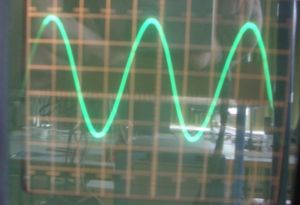
Oszilloskop
|
Auf einem Oszilloskop sieht man obiges Bild.
|
Der Biorhythmus
(Diese Aufgabe wird evtl. entsprechend umformuliert)
|
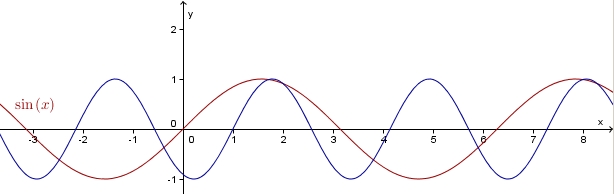
In dem unteren Bild sind der Graph der Sinusfunktion (rot) und ein weiterer Graph einer Sinusfunktion (schwarz) zu sehen.
|
Super! Nun hast du es geschafft und das Ende des Lernpfades erreicht.
Hefteintrag: Lese dir bitte deinen Hefteintrag durch und überprüfe kurz, ob du wirklich alle gelb hinterlegten Texte übernommen hast.
Nun hast du es wirklich geschafft. Du kannst stolz sein - gut gemacht! Ich wünsche dir noch einen schönen Tag!
zw:Trigonometrische Funktionen
(Diese Aufgaben werden evtl. noch gelöscht.)
- Hier kannst beide Parameter c und d von sin(x+c)+d durch Verschieben des Graphen ändern und die Auswirkung auf den Funktionsterm betrachten. Übertrage deine Ergebnisse auf cos(x+c)+d.
- In diesem Arbeitsblatt sollst du die zu den Graphen gehörenden Funktionsterme finden.
- Was fällt auf, wenn du hier für
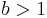 den Parameter
den Parameter  änderst?
änderst?
- In dem Applet auf dieser Seite werden die Parameter
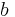 und
und  anders verwendet. Finde den Unterschied zu den bisherigen Betrachtungen heraus.
anders verwendet. Finde den Unterschied zu den bisherigen Betrachtungen heraus.
- Übertrage deine Ergebnisse auf a cos(bx+c)+d beziehungsweise a cos[b(x+c)]+d
- In dem Applet auf dieser Seite wird gezeigt, wie man eine Schwingung darstellen kann. Mit dem Schieberegler für t kannst du die Schwingung darstellen. Überlege dir die gestellten Aufgaben und finde dann mit den angegebenen Größen y_max und T einen Funktionsterm für die zugehörige Sinusschwingung.
- In dem Applet auf diesem Arbeitsblatt werden die Parameter einer Sinusschwingung aus der Physik behandelt. Welche Parameter a,b,c,d entsprechen welchen physikalischen Größen a, f, phi_0?
- In diesem Lernpfad zur harmonischen Schwingung findest du als Lernschritt 8 eine Aufgabe. Kannst du sie lösen? Fertige eine Zeichnung an! Finde die entsprechenden Größen a,b,c,d von a sin(b x - c)+d?

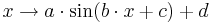 .
.
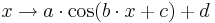 .
.
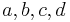 Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Im Folgenden seien
Parameter, die auf das Aussehen des Funktionsgraphen Einfluss nehmen. Im Folgenden seien 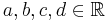 und
und 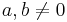 .
.
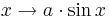 .
.
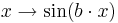 .
.
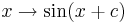 .
.
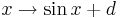 .
.
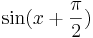 und
und 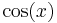 und
betrachte sie! Was fällt dir auf?
und
betrachte sie! Was fällt dir auf?
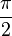 nach links verschiebt.
nach links verschiebt.