Potenzfunktionen - 1. Stufe: Unterschied zwischen den Versionen

Aus Medienvielfalt-Wiki
Wechseln zu: Navigation, Suche
(→‎Gerade Potenzen)
Zeile 27: Zeile 27:
 
Wir betrachten nun die Graphen der Funktionen mit f(x) = x<sup>n</sup>, wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..  
 
Wir betrachten nun die Graphen der Funktionen mit f(x) = x<sup>n</sup>, wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..  
  
−
{| class="prettytable sortable"  
+
{| <!--class="prettytable sortable" -->
 
|-  
 
|-  
 
| <ggb_applet height="450" width="450" showMenuBar="false" showResetIcon="true"  
 
| <ggb_applet height="450" width="450" showMenuBar="false" showResetIcon="true"  
Zeile 54: Zeile 54:
 
Wir betrachten jetzt die Funktionen mit f(x) = a*x<sup>n</sup>, n eine natürliche Zahl, a eine reelle Zahl.
 
Wir betrachten jetzt die Funktionen mit f(x) = a*x<sup>n</sup>, n eine natürliche Zahl, a eine reelle Zahl.
  
−
{| class="prettytable sortable"  
+
{| <!--class="prettytable sortable"-->
 
|-  
 
|-  
 
| <ggb_applet height="450" width="450" showMenuBar="false" showResetIcon="true"  
 
| <ggb_applet height="450" width="450" showMenuBar="false" showResetIcon="true"  
Zeile 66: Zeile 66:
  
  
−
{| class="prettytable sortable"  
+
{| <!--class="prettytable sortable"-->
 
|-  
 
|-  
 
| <ggb_applet height="450" width="450" showMenuBar="false" showResetIcon="true"  
 
| <ggb_applet height="450" width="450" showMenuBar="false" showResetIcon="true"  

Version vom 2. Januar 2009, 11:54 Uhr

Start -Einführung - 1. Stufe - 2. Stufe - 3. Stufe - 4. Stufe - 5. Stufe

Inhaltsverzeichnis

Die Graphen der Funktionen mit f(x) = xn, n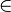 \in IN

Gerade Potenzen

Wir betrachten zunächst die Graphen der Funktionen mit f(x) = xn, wenn n eine gerade Zahl ist, als n = 2, 4, 6, ..

  Aufgabe 1  Stift.gif
  1. Beschreibe die Graphen! Achte dabei auf
    • Symmetrie
    • Monotonie
    • größte und kleinste Funktionswerte
  2. Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe! Zur Hilfe kannst du auch die Schar der Graphen zeichnen lassen.
  3. Beschreibe die Veränderung der Graphen beim Übergang von f(x) = x2 zu f(x) = x4, dann die beim Übergang von f(x) = x4 zu f(x) = x6 usw.!
  4. Wie ändern sich die y-Werte bei f(x) = xn, n gerade, wenn der x-Wert ver-k-facht wird? LÖSUNG!


Ungerade Potenzen

Wir betrachten nun die Graphen der Funktionen mit f(x) = xn, wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..

  Aufgabe 2  Stift.gif
  1. Beschreibe wieder die Graphen! Achte dabei auf
  • Symmetrie
  • Monotonie
  • größte und kleinste Funktionswerte
  1. Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe!
  2. Beschreibe die Veränderung der Graphen beim Übergang von f(x) = x1 zu f(x) = x3, dann die beim Übergang von f(x) = x3 zu f(x) = x5 usw.!

TESTE dein Wissen

  Aufgabe 3  Stift.gif

Wir betrachten die Funktionen mit f(x) = xn, n eine natürliche Zahl

  1. Für welches n verläuft der Graph durch den Punkt P(2;32)?
  2. Für welches n verläuft der Graph durch Q(1,5;3,375)?


Die Graphen von f(x) = a*xn, mit a 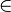\in IR

Wir betrachten jetzt die Funktionen mit f(x) = a*xn, n eine natürliche Zahl, a eine reelle Zahl.

  Aufgabe 4  Stift.gif
  1. Es sei zunächst n = 2, also f(x) = a*x2. Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
  2. Beschreibe die Veränderung der Graphen mit f(x) = a*xn bei der Veränderung des Parameter a ! Unterscheide dabei wieder zwischen geraden und ungeraden Exponenten.


  Aufgabe 5  Stift.gif

Wir betrachten wieder die Funktionen mit f(x) = a*xn, n eine natürliche Zahl

  1. Bestimme a und n so, dass der Graph durch die Punkte A(??;??) und B(??;??) verläuft. Nebenstehende Graphik dient als Hilfe. Die Punkte A und B kannst du frei verschieben.
  2. Bestimme a und n so, ....

TESTE dein Wissen

??????????????? Schön wäre ein Test wie bei der "Einführung"! ?????

Von „http://medienvielfalt.zum.de/index.php?title=Potenzfunktionen_-_1._Stufe&oldid=1634“