|
|
| Zeile 91: |
Zeile 91: |
| | }}<br> | | }}<br> |
| | :{{Lösung versteckt| | | :{{Lösung versteckt| |
| − | :1. a = -0.5, n = 3<br> | + | : 1. a = -0.5, n = 3<br> |
| − | :2. Es gibt keine Lösung, denn ....}} | + | : 2. Es gibt keine Lösung, denn ....}} |
| | |} | | |} |
| | | | |
Version vom 11. Januar 2009, 17:58 Uhr
Die Graphen der Funktionen mit f(x) = xn, n ∈ IN
Gerade Potenzen
Wir betrachten zunächst die Graphen der Funktionen mit f(x) = xn, wenn n eine gerade Zahl ist, also n = 2, 4, 6, ...
Aufgabe 1 
- Mit dem Schieberegler kannst du den Exponenten verändern. Beschreibe Gemeinsamkeiten und Unterschiede der Graphen! Achte dabei auf
- Symmetrie
- Monotonie
- größte und kleinste Funktionswerte
- Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe! Zur Hilfe kannst du auch die Schar der Graphen zeichnen lassen.
HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen
- Beschreibe die Veränderung der Graphen beim Übergang von f(x) = x2 zu f(x) = x4, dann die beim Übergang von f(x) = x4 zu f(x) = x6 usw.!
- Wie ändern sich die y-Werte bei f(x) = xn, n gerade, wenn der x-Wert ver-k-facht wird?
- [Lösung anzeigen][Lösung ausblenden]
- Wenn der x-Wert ver-k-facht wird, dann wird der y-Wert ver-kn-facht.
- Symbolisch
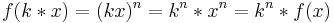 . .
|
|
|
Ungerade Potenzen
Wir betrachten nun die Graphen der Funktionen mit f(x) = xn, wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..
|
|
Aufgabe 2 
- Beschreibe wieder die Graphen! Achte dabei auf
- Symmetrie
- Monotonie
- größte und kleinste Funktionswerte
- Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe!
HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen
- Beschreibe die Veränderung der Graphen beim Übergang von f(x) = x1 zu f(x) = x3, dann die beim Übergang von f(x) = x3 zu f(x) = x5 usw.!
|
|
Teste dein Wissen
Die Graphen von f(x) = a*xn, mit a ∈ IR
Wir betrachten jetzt die Funktionen mit f(x) = a*xn, wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n ∈ IN, a ∈ IR .
Aufgabe 4 
- Es sei zunächst n = 2, also f(x) = a*x2. Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
- Beschreibe die Veränderung der Graphen mit f(x) = a*xn bei der Veränderung des Parameter a ! Unterscheide dabei wieder zwischen geraden und ungeraden Exponenten.
|
|
|
|
|
Aufgabe 5 
Wir betrachten wieder die Funktionen mit f(x) = a*xn, n eine natürliche Zahl
- Bestimme a und n so, dass der Graph durch die Punkte A(-2;4) und B(1;-0,5) verläuft. Nebenstehende Graphik dient als Hilfe. Die Punkte A und B kannst du frei verschieben.
- Bestimme a und n so, dass der Graph durch die Punkte A(-1;-1) und B(0,5;3) verläuft. Was fällt auf? Erkläre deine Beobachtungen.
|
}}
- [Lösung anzeigen][Lösung ausblenden]
{{{1}}}
|
Teste Dein Wissen
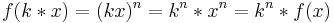 .
.
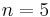 durchlaufen:
durchlaufen: 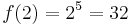 .
.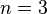 durchlaufen:
durchlaufen: 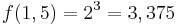 .
.

