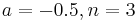Potenzfunktionen - 1. Stufe: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
| Zeile 52: | Zeile 52: | ||
# Für welches n verläuft der Graph durch Q(1,5;3,375)? | # Für welches n verläuft der Graph durch Q(1,5;3,375)? | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | :Der Punkt P(2;32) wird für <math>n=5</math> durchlaufen: <math>f (2) = 2^5 = 32</math>.<br> | + | :Der Punkt P(2;32) wird für <math>n=5</math> durchlaufen: <math>f \left( 2 \right ) = 2^5 = 32</math>.<br> |
| − | :Der Punkt Q(1,5;3,375) wird für <math>n=3</math> durchlaufen: <math>f (1,5) = 2^3 = 3,375</math>. | + | :Der Punkt Q(1,5;3,375) wird für <math>n=3</math> durchlaufen: <math>f \left( 1,5 \right ) = 2^3 = 3,375</math>. |
}} | }} | ||
}} | }} | ||
| Zeile 83: | Zeile 83: | ||
# Bestimme a und n so, dass der Graph durch die Punkte A(-1;-1) und B(0,5;3) verläuft. Was fällt auf? Erkläre deine Beobachtungen. | # Bestimme a und n so, dass der Graph durch die Punkte A(-1;-1) und B(0,5;3) verläuft. Was fällt auf? Erkläre deine Beobachtungen. | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | : 1. <math>a = -0.5, | + | : 1. <math>a = -0.5, n = 3</math><br> |
: 2. Es gibt keine Lösung, denn ...}} | : 2. Es gibt keine Lösung, denn ...}} | ||
}}<br> | }}<br> | ||
Version vom 13. Januar 2009, 19:08 Uhr
Inhaltsverzeichnis |
Die Graphen der Funktionen mit f(x) = xn, n ∈ IN
Gerade Potenzen
Wir betrachten zunächst die Graphen der Funktionen mit f(x) = xn, wenn n eine gerade Zahl ist, also n = 2, 4, 6, ...
|
Ungerade Potenzen
Wir betrachten nun die Graphen der Funktionen mit f(x) = xn, wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..
|
Teste dein Wissen
|
Wir betrachten die Funktionen mit f(x) = xn, n eine natürliche Zahl
|
Die Graphen von f(x) = a*xn, mit a ∈ IR
Wir betrachten jetzt die Funktionen mit f(x) = a*xn, wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n ∈ IN, a ∈ IR .
|
|
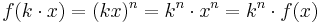 .
.
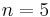 durchlaufen:
durchlaufen: 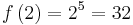 .
.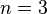 durchlaufen:
durchlaufen: 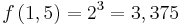 .
.
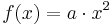 . Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
. Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
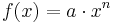 bei der Veränderung des Parameter a! Unterscheide dabei wieder zwischen geraden und ungeraden Exponenten.
bei der Veränderung des Parameter a! Unterscheide dabei wieder zwischen geraden und ungeraden Exponenten.