Bestimmung der Funktionsgleichung aus dem Graphen: Unterschied zwischen den Versionen
K (→Bestimmung einer Funktionsgleichung aus dem Graphen) |
K (→Bestimmung einer Funktionsgleichung aus dem Graphen) |
||
| Zeile 40: | Zeile 40: | ||
{{Arbeiten|NUMMER=4|ARBEIT= | {{Arbeiten|NUMMER=4|ARBEIT= | ||
# In diesem [http://www.mathe-online.at/mathint/fun2/applet_b_grapherk3.html Applet] kannst zu zeigen, ob du zu gegeben Graphen den zugehörigen Term findest. | # In diesem [http://www.mathe-online.at/mathint/fun2/applet_b_grapherk3.html Applet] kannst zu zeigen, ob du zu gegeben Graphen den zugehörigen Term findest. | ||
| − | # Gib einen Funktionsterm zu dem Graphen an, den man erhält falls die Sinuskurve um zwei nach links und um 3 nach oben verschoben wird! Wie lautet die Gleichung, falls zusätzlich die | + | # Gib einen Funktionsterm zu dem Graphen an, den man erhält falls die Sinuskurve um zwei nach links und um 3 nach oben verschoben wird! Wie lautet die Gleichung, falls zusätzlich die Periode halbiert werden soll?}} |
---- | ---- | ||
Version vom 19. Januar 2009, 18:51 Uhr
Einführung - Einfluss der Parameter - Bestimmung der Funktionsgleichung aus dem Graphen - Anwendungen in der Physik - Zusatzaufgaben
Informationen aus dem Graphen
|
|
|
Bestimmung einer Funktionsgleichung aus dem Graphen
Beachte, zu einem Graphen kann es mehrere zugehörige Funktionsgleichungen geben. D.h. die Antwort auf die Frage nach einer Funktionsgleichung zu einem gegebenen Graphen muss nicht immer eindeutig sein.
|
Um zu sehen wie man aus dem Graphen einer Funktion eine zugehörige Funktionsgleichung bestimmen kann, klicke in die leeren Kontrollkästchen. |
|
Bestimme zu folgenden Graphen je eine zugehörige Funktionsgleichung der Form |
Jetzt noch was zum Knobeln!!!
|
Lösung zu Aufgabe 1:
Amplitude: 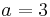
Wertemenge: ![W = [-3;\ 3]](/images/math/7/f/4/7f4a584468ac15313bbdcbd41602ca3e.png)
Periode: 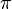
Nullstellen: 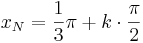 mit
mit  oder
oder 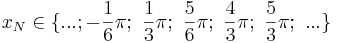
Tiefpunkte: 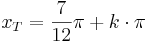 mit
mit  oder
oder 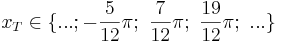
Hochpunkte: 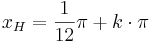 mit
mit  oder
oder 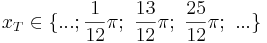
streng monoton fallend: ![...;\ [\frac{1}{12}\pi;\ \frac{7}{12}\pi];\ [\frac{13}{12}\pi;\ \frac{19}{12}\pi];\ ...](/images/math/2/3/5/2352ffad5112a215b1551af34791f362.png)
![...;\ [-\frac{5}{12}\pi;\ \frac{1}{12}\pi];\ [\frac{7}{12}\pi;\ \frac{13}{12}\pi];\ [\frac{19}{12}\pi;\ \frac{25}{12}\pi];\ ...](/images/math/a/b/3/ab3f03ffd65ea28a0ffd4a78e3cd5295.png)
Lösung zu Aufgabe 3: Hier kannst Du überprüfen, ob deine Ergebnisse stimmen. Stelle dazu die Schieberegler entsprechend ein.
Lösung zu Aufgabe 4:
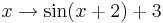 und
und 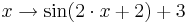
Weiter geht es mit
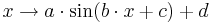 .
.

