Einfluss von c: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
K |
K |
||
| Zeile 87: | Zeile 87: | ||
''Lösung zu Aufgabe C''3: {{versteckt| | ''Lösung zu Aufgabe C''3: {{versteckt| | ||
Eine mögliche Begründung: | Eine mögliche Begründung: | ||
| − | <math> y = \sin ( x + c ) </math> | + | |
| + | <math> y = \sin ( x + c ) </math>, | ||
| + | |||
d.h. jeder Funktionswert wird bereits ein Stück weiter links angenommen. | d.h. jeder Funktionswert wird bereits ein Stück weiter links angenommen. | ||
}} | }} | ||
Version vom 20. Januar 2009, 16:23 Uhr
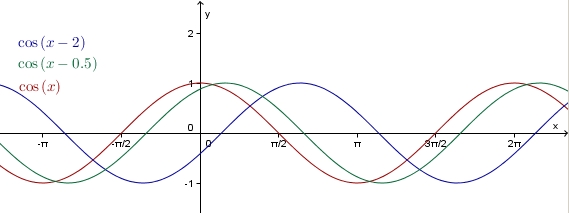
Wir betrachten nun den Einfluss von  in
in
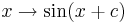 .
.
|
|
Nun betrachten wir den Einfluss von  in
in
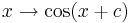 .
.
|
Öffne dieses GeoGebra-Applet und bearbeite damit obige Aufgaben eins bis vier nochmals.
|
|
Versuche nun die beobachteten Veränderungen auch mathematisch zu begründen! |
Lösung zu Aufgabe C1:
{{{1}}}
Lösung zu Aufgabe C2:
Die allgemeine Kosinusfunktion verhält sich bei Variation von  genauso wie die allgemeine Sinusfunktion.
genauso wie die allgemeine Sinusfunktion.
Lösung zu Aufgabe C3:
Eine mögliche Begründung:
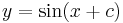 ,
,
d.h. jeder Funktionswert wird bereits ein Stück weiter links angenommen.
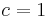 ein. Wie ändert sich der Graph?
ein. Wie ändert sich der Graph? 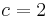 und
und 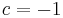 , sowie
, sowie 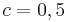 und
und 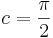 auf den Graphen auswirken und überprüfe Deine Vermutung.
auf den Graphen auswirken und überprüfe Deine Vermutung.