Potenzfunktionen - 3. Stufe: Unterschied zwischen den Versionen

Version vom 25. Januar 2009, 11:42 Uhr

Start - Einführung - 1. Stufe - 2. Stufe - 3. Stufe - 4. Stufe - 5. Stufe

Inhaltsverzeichnis

1 Die Graphen der Funktionen mit f(x) = x^1/n, n ∈ IN
- 1.1 Vergleiche mit Funktionen aus Stufe 2
2 Potenzen und Wurzeln
3 Definitionsbereich der Wurzelfunktionen
- 3.1 Einschränkung auf IR⁺
- 3.2 Wurzelfunktion auf ganz IR

Die Graphen der Funktionen mit f(x) = x^1/n, n ∈ IN

Es sei stets IN₀={0,1,2,...} und IN={1,2,3,..}, insbesondere also IN₀ =/= IN.
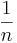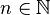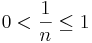Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen positiven Stammbruch der Form $\frac{1}{n}$ mit $n \in \mathbb{N}$ als Exponenten haben. Während in Stufe 1 und 2 dieses Kurses die Exponenten stets ganzzahlig waren, gilt für die Stammbrüche: $0<\frac{1}{n}\leq 1$ .

Vergleiche mit Funktionen aus Stufe 2

Aufgabe 1

Verleiche den neuen Graphen mit dem, den Du schon aus Stufe 1 und 2 dieses Kurses kennst (gestrichelt).
Mit dem Schieberegler kannst du wieder die Exponenten verändern.
Beschreibe Gemeinsamkeiten und Unterschiede der Graphen! Achte dabei auf
- Symmetrie
- Monotonie
- größte und kleinste Funktionswerte
Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe! Zur Hilfe kannst du auch die Schar der Graphen zeichnen lassen.
```
HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen 
```
Beschreibe die Veränderung der Graphen beim Übergang von f(x) = x² zu f(x) = x⁴, dann die beim Übergang von f(x) = x⁴ zu f(x) = x⁶ usw.!
Wie ändern sich die y-Werte bei f(x) = xⁿ, n gerade, wenn der x-Wert ver-k-facht wird?

Wenn der x-Wert ver-k-facht wird, dann wird der y-Wert ver-kⁿ-facht.

Symbolisch $f(k \cdot x) = (kx)^n = k^n \cdot x^n = k^n \cdot f(x)$ .

Welche Gemeinsamkeiten gibt es? Welche Unterschiede?
Gibt es Punkte, die beiden Funktionsscharen gemeinsam sind?

Beschreibe den Definitionsbreich ID der Funktion f(x) = x^(1/n) in Abhängigkeit von n.

Potenzen und Wurzeln

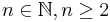Eine Funktion $f$ mit der Gleichung $f(x)=\sqrt[n]{x}$ mit $n \in \mathbb{N}, n\geq2$ heißt Wurzelfunktion.

Potenzfunktionen der Bauart 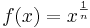$f(x)=x^{\frac{1}{n}}$ und Wurzelfunktionen $g(x)=\sqrt[n]{x}$ hängen eng zusammen, denn es gilt:

$x^{\frac{1}{n}}:=\sqrt[n]{x}$

Darin ist die n-te Wurzel festgelegt über:

$\sqrt[n]{x} :\Leftrightarrow \left(\sqrt[n]{x}\right)^n = x$

Beispiele:

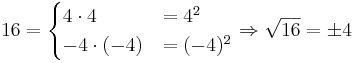$16 = \begin{cases} 4\cdot 4 &= 4^2\\ -4 \cdot (-4) &= (-4)^2 \end{cases} \Rightarrow \sqrt{16} = \pm 4$ , aber
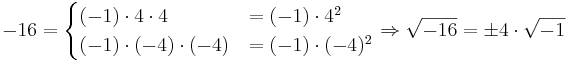$-16 = \begin{cases} (-1)\cdot 4\cdot 4 &= (-1)\cdot 4^2\\ (-1)\cdot (-4) \cdot (-4) &= (-1)\cdot (-4)^2 \end{cases} \Rightarrow \sqrt{-16}=\pm 4\cdot\sqrt{-1}$ , nicht definiert.
$\sqrt[3]{27}=\sqrt[3]{3\cdot 3 \cdot 3} = \sqrt[3]{3^3} = \sqrt[3]{3}^3 = 3$ , aber auch

Definitionsbereich der Wurzelfunktionen

Einschränkung auf IR⁺

Offenbar kann man zum Beispiel wegen

$\sqrt[3]{-27}=\sqrt[3]{-3\cdot -3 \cdot -3} = \sqrt[3]{-3^3} = \sqrt[3]{-3}^3 = -3$ , und
$\sqrt[3]{ 27}=\sqrt[3]{3\cdot 3 \cdot 3} = \sqrt[3]{3^3} = \sqrt[3]{3}^3 = 3$

die Wurzelfunktionen $f(x)=\sqrt[n]{x}$ zumindest bei ungeradem n sowohl für positive als auch negative x definieren.

Allerdings kann das zu Wiedersprüchen führen; folgende Rechnung zeigt die Problematik:

$-2 = \sqrt[3]{-8} = (-8)^{\frac{1}{3}} = (-8)^{\frac{2}{6}} = \left( (-8)^2 \right)^{\frac{1}{6}} = = \left( (8)^2 \right)^{\frac{1}{6}} = (8)^{\frac{2}{6}} = (8)^{\frac{1}{3}} = \sqrt[3]{8} = 2.$

Um solche Fälle von Nicht-Eindeutigkeit zu umgehen, schränkt man den Definitionsbereich ID der Wurzelfunktionen i.d.R. grundsätzlich auf die positiven reelle Zahlen ein, also:

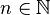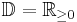
$f(x) = \sqrt[n]{x}$ mit $n \in \mathbb{N}$ und $\mathbb{D}=\mathbb{R}_{\geq 0}$

Wurzelfunktion auf ganz IR

Will man eine Wurzelfunktion dennoch auf ganz IR definieren (d.h. ID = IR), dann muss man sie - nach obiger Vorüberlegung - aus zwei einzelnen Wurzelfunktionen zusammensetzen. Man definiere etwa g(x) derart, dass

$g(x):=\begin{cases}\sqrt[n]{x}, &x\geq 0 \\ -\sqrt[n]{-x}, &x<0\end{cases}$ . Dann gilt: ID_g = IR.

@@ Zeile 8: / Zeile 8: @@
 === Vergleiche mit Funktionen aus Stufe 2 ===
+{| cellspacing="10"
+|- style="vertical-align:top;"
+| {{Arbeiten|NUMMER=1|ARBEIT=
+# Verleiche den neuen Graphen mit dem, den Du schon aus Stufe 1 und 2 dieses Kurses kennst (gestrichelt).
+# Mit dem Schieberegler kannst du wieder die Exponenten verändern.
+# Beschreibe Gemeinsamkeiten und Unterschiede der Graphen! Achte dabei auf
+#* Symmetrie
+#* Monotonie
+#* größte und kleinste Funktionswerte
+# Gibt es Punkte, die allen Graphen gemeinsam sind? Begründe! Zur Hilfe kannst du auch die Schar der Graphen zeichnen lassen. <br> <pre>HINWEIS: Rechtsklick auf Graph - "Spur an" auswählen </pre>
+# Beschreibe die Veränderung der Graphen beim Übergang von f(x) = x<sup>2</sup> zu f(x) = x<sup>4</sup>, dann die beim Übergang von f(x) = x<sup>4</sup> zu f(x) = x<sup>6</sup> usw.!
+# Wie ändern sich die y-Werte bei f(x) = x<sup>n</sup>, n gerade, wenn der x-Wert ver-k-facht wird?
+:{{Lösung versteckt|
+:Wenn der x-Wert ver-k-facht wird, dann wird der y-Wert ver-k<sup>n</sup>-facht. <br>
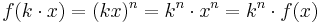+:Symbolisch <math>f(k \cdot x) = (kx)^n = k^n \cdot x^n = k^n \cdot f(x)</math>.
+}}
+}}<br>
+|| <ggb_applet height="300" width="350" showMenuBar="false" showResetIcon="true"
+filename="3_gerade_xn.ggb" />
+|}
 * Welche Gemeinsamkeiten gibt es? Welche Unterschiede?
@@ Zeile 18: / Zeile 40: @@
 filename="7_x1n.ggb" />
-<ggb_applet height="450" width="600" showMenuBar="false" showResetIcon="true"
-filename="test.ggb" /><br /><br />
-{{ggb|test.ggb|Datei}}
 == Potenzen und Wurzeln ==

Potenzfunktionen - 3. Stufe: Unterschied zwischen den Versionen

Version vom 25. Januar 2009, 11:42 Uhr

Inhaltsverzeichnis