Potenzfunktionen - 4. Stufe: Unterschied zwischen den Versionen
K (→test zone) |
K (→test zone) |
||
| Zeile 90: | Zeile 90: | ||
\begin{matrix} | \begin{matrix} | ||
f(n+1)&=& (n+1)^2 \\ | f(n+1)&=& (n+1)^2 \\ | ||
| − | + | \, &=& n^2 + 2n + 1 | |
end{matrix} | end{matrix} | ||
</math> | </math> | ||
Version vom 29. Januar 2009, 10:43 Uhr
Inhaltsverzeichnis |
Die Graphen der Funktionen mit f(x) = x-1/n, n ∈ IN
Es sei stets IN0={0,1,2,...} und IN={1,2,3,..}, insbesondere also IN0 =/= IN.
Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen negativen Stammbruch der Form 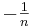 mit
mit 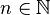 als Exponenten haben. Für diese Art der Exponenten gilt:
als Exponenten haben. Für diese Art der Exponenten gilt: 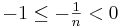 .
.
Vergleich mit Funktionen aus Stufe 3
|
Exponenten, Brüche und Potenzgesetze
Im vorliegenden Fall betrachten wir negative Stammbrüche als Exponten. Man erinnere sich dabei an die Potenzgesetze, insbesondere an folgenden Zusammenhang:
- Für eine reelle Zahl
 und eine natürliche Zahl
und eine natürliche Zahl 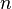 wird definiert:
wird definiert:
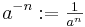 für
für 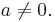
Auf unsere Situation angewandt ergibt sich:
|
Potenzfunktionen und ihre Umkehrfunktionen
Beispiel
Es sei  eine Potenzfunktion, definiert durch
eine Potenzfunktion, definiert durch 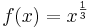 . Gesucht ist die Umkehrfunktion
. Gesucht ist die Umkehrfunktion 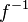 von
von  (man beachte die unterschiedliche Bedeutung von
(man beachte die unterschiedliche Bedeutung von 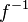 und
und 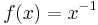 !).
!).
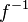 ergibt sich aus
ergibt sich aus  durch Auflösen nach
durch Auflösen nach  . Es ist:
. Es ist:
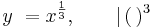
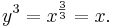
Beispiel
Es sei  eine Potenzfunktion, nun definiert durch
eine Potenzfunktion, nun definiert durch 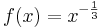 mit Definitionsbereich ID = IR+. Gesucht ist wieder ihre Umkehrfunktion
mit Definitionsbereich ID = IR+. Gesucht ist wieder ihre Umkehrfunktion 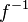 .
.
Auflösen nach  ergibt:
ergibt:
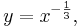
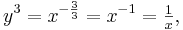
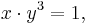
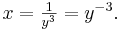
Was bewirken Parameter in Potenzfunktionen? - Merkregel "5 S"
- Spiegeln
- Strecken
- Stauchen
- Schieben
- Superponieren
Siehe Video auf www.oberprima.com.
APPLET
test zone
Fehler beim Parsen(Syntaxfehler): \begin{matrix} f(n+1)&=& (n+1)^2 \\ \, &=& n^2 + 2n + 1 end{matrix}
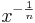
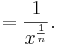
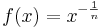 den Definitonsbereich D = IR+.
den Definitonsbereich D = IR+.
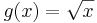 nur auf IR+ definiert, das heißt ihr Definitionsbereich
nur auf IR+ definiert, das heißt ihr Definitionsbereich  IR+.
IR+.![f(x) = x^{-\frac 1 n}= \textstyle \frac{1}{x^{\frac 1 n}} = \textstyle \frac{1}{\sqrt[n]{x}} = \textstyle \frac{1}{g(x)}](/images/math/d/f/f/dffb5aedde565c318a02642cbcd56b38.png) überträgt sich der Definitionsbereich der Funktion g auf die Funktion f.
überträgt sich der Definitionsbereich der Funktion g auf die Funktion f.
