Potenzfunktionen - 2. Stufe: Unterschied zwischen den Versionen
(→Ungerade Potenzen: - parabel & hyperbel) |
(→Parabel und Hyperbel) |
||
| Zeile 32: | Zeile 32: | ||
Du hat nun Potenzfunktionen der Bauart <math>f(x)=x^n</math> und <math>f(x)=x^{-n}</math> kennengelernt. Ihre Graphen spielen in der Mahtematik und in den Naturwissenschaften eine wichtige Rolle und haben deshalb eigene Bezeichnungen: | Du hat nun Potenzfunktionen der Bauart <math>f(x)=x^n</math> und <math>f(x)=x^{-n}</math> kennengelernt. Ihre Graphen spielen in der Mahtematik und in den Naturwissenschaften eine wichtige Rolle und haben deshalb eigene Bezeichnungen: | ||
| − | Die Graphen von Funktionen der Form f(x)=x^n mit einer natürlichen Zahl n heißen '''Parabeln'''. Ist f(x)=x^2, dann heißt der Graph Normalparabel; wenn f(x)=x^3 dann nennt man den Graphen '''kubische Grundparabel''' (oder '''Parabel dritter Ordnung'''). | + | Die Graphen von Funktionen der Form <math>f(x)=x^n</math> mit einer natürlichen Zahl n heißen '''Parabeln''', oder genauer: <math>Parabel n-ter Ordnung</math>. Ist <math>f(x)=x^2</math>, dann heißt der Graph Normalparabel; wenn <math>f(x)=x^3</math> dann nennt man den Graphen '''kubische Grundparabel''' (oder '''Parabel dritter Ordnung'''). |
| − | Die Graphen von Funktionen der Form f(x)=x^{-n} mit einer natürlichen Zahl n heißen '''Hyperbeln'''. Hyperbeln haben stets je zwei Asymptoden, die auch die Lücken in Definitions- und Wertemenge beschreiben. | + | Die Graphen von Funktionen der Form <math>f(x)=x^{-n}</math> mit einer natürlichen Zahl n heißen '''Hyperbeln (n-ter Ordnung)'''. Hyperbeln haben stets je zwei Asymptoden, die auch die Lücken in Definitions- und Wertemenge beschreiben. |
<span style="color: RED">XXX ZUSATZINFO ENDE XXX (JW)</span> | <span style="color: RED">XXX ZUSATZINFO ENDE XXX (JW)</span> | ||
| − | |||
| − | |||
=== Ungerade Potenzen === | === Ungerade Potenzen === | ||
Version vom 2. Februar 2009, 12:46 Uhr
Inhaltsverzeichnis |
Die Graphen der Funktionen mit f(x) = x-n, n ∈ IN
Gerade Potenzen
Wir betrachten zunächst die Graphen der Funktionen mit f(x) = x-n, wenn n eine gerade Zahl ist, also n = 2, 4, 6, ...
|
Parabel und Hyperbel
XXX ZUSATZINFO EINFÜGEN? XXX (JW)
Du hat nun Potenzfunktionen der Bauart 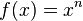 und
und 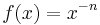 kennengelernt. Ihre Graphen spielen in der Mahtematik und in den Naturwissenschaften eine wichtige Rolle und haben deshalb eigene Bezeichnungen:
kennengelernt. Ihre Graphen spielen in der Mahtematik und in den Naturwissenschaften eine wichtige Rolle und haben deshalb eigene Bezeichnungen:
Die Graphen von Funktionen der Form 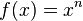 mit einer natürlichen Zahl n heißen Parabeln, oder genauer:
mit einer natürlichen Zahl n heißen Parabeln, oder genauer: 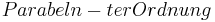 . Ist
. Ist 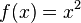 , dann heißt der Graph Normalparabel; wenn
, dann heißt der Graph Normalparabel; wenn 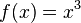 dann nennt man den Graphen kubische Grundparabel (oder Parabel dritter Ordnung).
dann nennt man den Graphen kubische Grundparabel (oder Parabel dritter Ordnung).
Die Graphen von Funktionen der Form 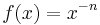 mit einer natürlichen Zahl n heißen Hyperbeln (n-ter Ordnung). Hyperbeln haben stets je zwei Asymptoden, die auch die Lücken in Definitions- und Wertemenge beschreiben.
mit einer natürlichen Zahl n heißen Hyperbeln (n-ter Ordnung). Hyperbeln haben stets je zwei Asymptoden, die auch die Lücken in Definitions- und Wertemenge beschreiben.
XXX ZUSATZINFO ENDE XXX (JW)
Ungerade Potenzen
Wir betrachten nun die Graphen der Funktionen mit 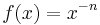 , wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..
, wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..
|
Teste dein Wissen
|
Wir betrachten die Funktionen mit f(x) = x-n, n eine natürliche Zahl
|
Die Graphen von f(x) = a*x-n, mit a ∈ IR
Wir betrachten jetzt die Funktionen mit 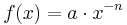 , wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n ∈ IN, a ∈ IR .
, wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n ∈ IN, a ∈ IR .
|
|
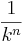 -facht.
-facht. 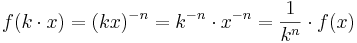 .
.
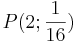
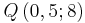 ?
?
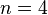 , dann gilt nämlich
, dann gilt nämlich 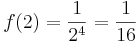 .
.
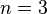 , dann gilt nämlich
, dann gilt nämlich 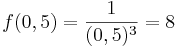
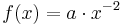 . Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
. Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
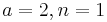 .
.

