|
|
| Zeile 63: |
Zeile 63: |
| | |} | | |} |
| | | | |
| − | {{ggb|12_axpq2.ggb|datei}} | + | <!-- {{ggb|12_axpq2.ggb|datei}} --> |
Version vom 20. Februar 2009, 23:20 Uhr
Die Graphen der Funktionen mit f(x) = xp/q, p ∈ Z und q ∈ IN
Wir betrachten in diesem Abschnitt die Graphen solcher Funktionen, die einen Bruch der Form 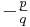 mit
mit 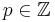 und
und 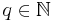 als Exponenten haben. Man spricht dann von Potenzfunktionen mit gebrochen rationalem Exponenten.
als Exponenten haben. Man spricht dann von Potenzfunktionen mit gebrochen rationalem Exponenten.
Vergleich mit Funktionen aus vorangegangenen Stufen
Aufgabe 1 
Verleiche den neuen Graphen (blau) mit dem, den Du schon aus vorangegangenen Stufen dieses Kurses kennst (rot und lila gestrichelt); mit dem Schieberegler kannst Du dazu wieder die Exponenten verändern.
- Beschreibe Gemeinsamkeiten und Unterschiede der Graphen! Achte dabei auf
- Definitionsbereich
- Symmetrie
- [Lösung anzeigen][Lösung ausblenden]
- Ist der Nenner im vollständig gekürzten Bruch gerade, so ist der Definitionsbereich auf
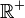 eingeschränkt. Bei allen anderen Funktionen ist der Definitionsbereich eingeschränkt. Bei allen anderen Funktionen ist der Definitionsbereich 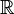 . .
- Wenn der Exponent vollständig gekürzt
- einen geraden Zähler besitzt, ist der Graph der Funktion achsensymmetrisch.
- einen geraden Nenner besitzt, ist der Graph nicht symmetrisch, da nur für
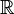 definiert. definiert.
- ungeraden Zähler und Nenner besitzt, ist der Graph punktsymmetrisch.
- Welche neuen Funktionen erhält mann, wenn man bei den Exponenten der Funktione auch für den Nenner ganze Zahlen statt nur natürliche Zahlen erlaubt, also wenn gilt f(x) = xp/q mit
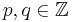 ? ?
- [Lösung anzeigen][Lösung ausblenden]
- Man erhält keine neuen Funktionen, wenn man auch für den Nenner des Exponenten negative Zahlen einsetzt. Denn der Exponent bleibt weiterhin ein Bruch und kann positiv oder negativ werden. Das kann aber bereits erreicht werden, indem im Zähler eine ganze Zahl
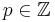 und im Nenner eine natürliche Zahl und im Nenner eine natürliche Zahl 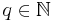 steht. steht.
|
|
|
Die Graphen der Potenzfunktion mit f(x) = a xp/q
Fasst man alle Variationsmöglichkeiten der Potenzfunktion der vorangegangenen Stufen zusammen, so erhält man die Potenzfunktion f(x) = a xp/q mit den Variablen 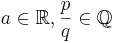 .
.
Aufgabe 2 
- Welchen der nebenstehenden Schieberegler für a, p und q muss man verändern, damit man
- eine Hyperbel
- eine Parabel
- einen monoton fallenden Graphen
- eine monton fallende Gerade
erhält, während die anderen beiden Schieberegler auf 1 bleiben.
- [Lösung anzeigen][Lösung ausblenden]
- Eine Hyperbel erhält man, wenn der Exponent negativ ist. Schieberegler p kleiner 0.
- Eine Parabel erhält man, wenn der Exponent 2 ist. Schieberegler p auf 2.
- Einen monoton fallenden Graphen erhält man, wenn a positiv und der Exponentenzähler p eine negative ungerade Zahl ist (punktsymmetrische Hyperbel) oder a negativ ist (monoton fallende Gerade).
- Bei einer monoton fallenden Gerade muss der Exponent 1 sein, also muss hier der Schieberegler a kleiner 0 eingestellt werden.
- Beschreibe zu verschiedenen Funktionen f(x)=1 xp/q die Veränderung des Graphen, wenn a>1 oder a<0 ist.
|
|
|
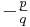 mit
mit 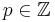 und
und 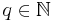 als Exponenten haben. Man spricht dann von Potenzfunktionen mit gebrochen rationalem Exponenten.
als Exponenten haben. Man spricht dann von Potenzfunktionen mit gebrochen rationalem Exponenten.
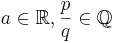 .
.
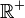 eingeschränkt. Bei allen anderen Funktionen ist der Definitionsbereich
eingeschränkt. Bei allen anderen Funktionen ist der Definitionsbereich 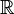 .
.
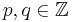 ?
?
