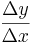Diskret - kontinuierlich: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(→Begriffsbildung) |
(→Begriffsbildung) |
||
| Zeile 18: | Zeile 18: | ||
Eine Differenzengleichung ist eine Möglichkeit, dynamische Systeme abzubilden. Dabei wird eine Folge von diskreten (einzeln betrachtbaren - "abzählbaren") Ereignissen rekursiv definiert. Jedes Folgenglied ist daher eine Funktion der vorhergehenden Folgenglieder. | Eine Differenzengleichung ist eine Möglichkeit, dynamische Systeme abzubilden. Dabei wird eine Folge von diskreten (einzeln betrachtbaren - "abzählbaren") Ereignissen rekursiv definiert. Jedes Folgenglied ist daher eine Funktion der vorhergehenden Folgenglieder. | ||
| − | Form: <math>x_{n}=f(x_{n-1},x_{n-2},..., | + | Form: <math>x_{n} = f(x_{n-1},x_{n-2},...,x_{1},x_{0})</math><br /> |
für natürliche Zahlen n. | für natürliche Zahlen n. | ||
Die Veränderung wird durch den '''Differenzenquotienten''' angegeben: | Die Veränderung wird durch den '''Differenzenquotienten''' angegeben: | ||
| − | <math>{ | + | <math>\frac{\Delta y}{\Delta x}</math> |
=== Marktgleichgewicht - Cobweb-DIagramm === | === Marktgleichgewicht - Cobweb-DIagramm === | ||
Version vom 28. März 2009, 15:12 Uhr
|
Über diesen Lernpfad
Schüler/innen sollen sich mit der Beschreibung von dynamischen Vorgängen beschäftigen und den Unterschied zwischen diskreten Vorgängen (Beschreibung über Differenzengleichungen) und kontinuierlichen Vorgängen (Beschreibung über Differentialgleichungen) kennen lernen. Kompetenzen
|
Inhaltsverzeichnis |
Rekursive Beschreibung von Veränderungen
Numerische Näherung - Heronverfahren
Radioaktiver Zerfall
Räuber-Beute-Modell
Differenzengleichung
Begriffsbildung
Eine Differenzengleichung ist eine Möglichkeit, dynamische Systeme abzubilden. Dabei wird eine Folge von diskreten (einzeln betrachtbaren - "abzählbaren") Ereignissen rekursiv definiert. Jedes Folgenglied ist daher eine Funktion der vorhergehenden Folgenglieder.
Form: 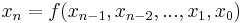
für natürliche Zahlen n.
Die Veränderung wird durch den Differenzenquotienten angegeben: