Diskret - kontinuierlich: Unterschied zwischen den Versionen
(→Radioaktiver Zerfall - analytische Herleitung) |
(→Begriffsbildung) |
||
| Zeile 66: | Zeile 66: | ||
== Differentialgleichungen == | == Differentialgleichungen == | ||
=== Begriffsbildung === | === Begriffsbildung === | ||
| + | Links: | ||
| + | * [http://statmath.wu-wien.ac.at/~leydold/MOK/HTML/node175.html http://statmath.wu-wien.ac.at/~leydold/MOK/HTML/node175.html], Josef Leydold, Abt. f. angewandte Statistik und Datenverarbeitung, 1997 | ||
| + | |||
=== Lösung einfacher Differentialgleichungen === | === Lösung einfacher Differentialgleichungen === | ||
Version vom 28. März 2009, 16:03 Uhr
|
Über diesen Lernpfad
Schüler/innen sollen sich mit der Beschreibung von dynamischen Vorgängen beschäftigen und den Unterschied zwischen diskreten Vorgängen (Beschreibung über Differenzengleichungen) und kontinuierlichen Vorgängen (Beschreibung über Differentialgleichungen) kennen lernen. Kompetenzen
|
Inhaltsverzeichnis |
Rekursive Beschreibung von Veränderungen
Numerische Näherung - Heronverfahren
Radioaktiver Zerfall
Räuber-Beute-Modell
Differenzengleichung
Begriffsbildung
Eine Differenzengleichung ist eine Möglichkeit, dynamische Systeme abzubilden. Dabei wird eine Folge von diskreten (einzeln betrachtbaren - "abzählbaren") Ereignissen rekursiv definiert. Jedes Folgenglied ist daher eine Funktion der vorhergehenden Folgenglieder.
Form: 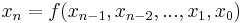
für natürliche Zahlen n.
Die Veränderung wird durch den Differenzenquotienten angegeben:
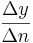
mit 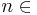 N
N
Dabei entspricht:
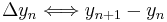 und damit beispielsweise
und damit beispielsweise 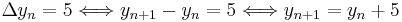
Links:
- http://statmath.wu-wien.ac.at/~leydold/MOK/HTML/node187.html, Josef Leydold, Abt. f. angewandte Statistik und Datenverarbeitung, 1997
Marktgleichgewicht - Cobweb-DIagramm
Cobweb / Spinnwebdiagramme stellen eine gute Möglichkeit dar, Rekursionen darzustellen. Links:
- Spinnwebdiagramme - Lineare Differenzengleichungen 1. Ordnung mit GeoGebra: http://www.geogebra.org/de/wiki/index.php/Lineare_Differenzengleichung_1._Ordnung
Von der diskreten zur kontinuierlichen Veränderung
Exponentielles Wachstum - Lebensmittelkontrolle
Radioaktiver Zerfall - analytische Herleitung
|
Gegeben ist die Funktion |
Aufgaben im pdf-Format
Die Angaben zu den Aufgaben findet man unter Integrationsmethoden_mv.pdf (41 kb).
Lösungen im pdf-Format
Die Lösungen zu diesen Aufgaben findet man unter Lösungen zu Integrationsmethoden_mv.pdf (117 kb).
Abbau von Giftstoffen
Logistisches Wachstum - beschränktes Wachstum
Ein-Lebewesen-Modell nach Verhulst
Differentialgleichungen
Begriffsbildung
Links:
- http://statmath.wu-wien.ac.at/~leydold/MOK/HTML/node175.html, Josef Leydold, Abt. f. angewandte Statistik und Datenverarbeitung, 1997
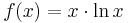 . Es gilt
. Es gilt 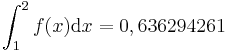 FE.
FE.

