Potenzfunktionen - 2. Stufe: Unterschied zwischen den Versionen
Aus Medienvielfalt-Wiki
(Lösung zu Aufgabe 1.2 eingef. + Layout) |
K (Rechtschreibf.) |
||
| Zeile 72: | Zeile 72: | ||
{{Arbeiten|NUMMER=3|ARBEIT= | {{Arbeiten|NUMMER=3|ARBEIT= | ||
Wir betrachten die Funktionen mit f(x) = x<sup>-n</sup>, n eine natürliche Zahl | Wir betrachten die Funktionen mit f(x) = x<sup>-n</sup>, n eine natürliche Zahl | ||
| − | # Für welches n verläuft der Graph durch den Punkt <math>P(2;\textstyle \frac{1}{16})</math> | + | # Für welches n verläuft der Graph durch den Punkt <math>P(2;\textstyle \frac{1}{16})</math>? |
# Für welches n verläuft der Graph durch <math>Q ( 0,\!5;8 )</math>? | # Für welches n verläuft der Graph durch <math>Q ( 0,\!5;8 )</math>? | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
Version vom 31. März 2009, 15:51 Uhr
Inhaltsverzeichnis |
Die Graphen der Funktionen mit f(x) = x-n, n ∈ IN
Gerade Potenzen
Wir betrachten zunächst die Graphen der Funktionen mit f(x) = x-n, wenn n eine gerade Zahl ist, also n = 2, 4, 6, ...
|
Parabel und Hyperbel
Du hast nun Potenzfunktionen mit den Gleichungen 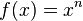 und
und 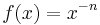 kennengelernt. Ihre Graphen spielen in der Mathematik und in den Naturwissenschaften eine wichtige Rolle. Sie haben deshalb eigene Bezeichnungen:
kennengelernt. Ihre Graphen spielen in der Mathematik und in den Naturwissenschaften eine wichtige Rolle. Sie haben deshalb eigene Bezeichnungen:
|
Merke:
|
Ungerade Potenzen
Wir betrachten nun die Graphen der Funktionen mit 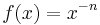 , wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..
, wenn n eine ungerade Zahl ist, also n = 1, 3, 5, ..
|
Teste dein Wissen
|
Wir betrachten die Funktionen mit f(x) = x-n, n eine natürliche Zahl
|
Die Graphen von f(x) = a x-n mit a ∈ IR
Wir betrachten jetzt die Funktionen mit 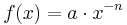 , wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n ∈ IN, a ∈ IR .
, wenn n eine natürliche Zahl und a eine reelle Zahl ist, also n ∈ IN, a ∈ IR .
|
|
Teste Dein Wissen
- Ordne dem Graphen der Potenzfunktion die richtige Gleichung zu!
- Erkenne die Art der Funktion und ordne dem Graphen die entsprechende Funktionsgleichung zu!

|
Als nächstes erfährst du etwas über Potenzfunktionen, die Stammbrüche im Exponenten haben. |
![]-\infty;0[](/images/math/b/5/0/b506be48eafe7c01cce18da0d9f808f4.png) streng monoton steigend und im Intervall
streng monoton steigend und im Intervall ![]0;\infty[](/images/math/d/c/f/dcfb1c7331a6972af80f5df85fdfb44d.png) streng monoton fallend.
streng monoton fallend.
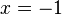 ist
ist 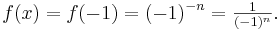 Da wir hier nur gerade Zahlen
Da wir hier nur gerade Zahlen 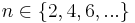 betrachten gilt weiter:
betrachten gilt weiter: 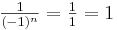 unabhängig von n.
unabhängig von n.
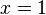 ist
ist 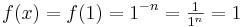 für alle
für alle 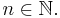
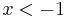 bzw.
bzw. 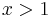 werden die Funktionswerte größer.
werden die Funktionswerte größer.
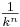 -facht.
-facht. 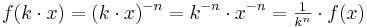 .
.
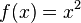 heißt der Graph Normalparabel; für
heißt der Graph Normalparabel; für 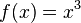 dann nennt man den Graphen kubische Grundparabel (oder Parabel dritter Ordnung).
dann nennt man den Graphen kubische Grundparabel (oder Parabel dritter Ordnung).
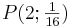 ?
?
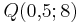 ?
?
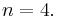
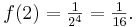
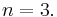
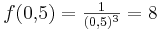
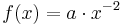 . Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
. Beschreibe die Veränderung des Graphen von f bei der Veränderung des Parameters a!
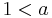 wird der Graph der Funktion gestreckt und wird für
wird der Graph der Funktion gestreckt und wird für 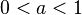 gestaucht.
gestaucht.
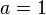 bleibt er unverändert
bleibt er unverändert
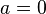 wird die Funktion zur Nullfunktion mit
wird die Funktion zur Nullfunktion mit 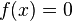 für alle
für alle  .
.
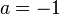 bewirkt eine Spiegelung des Graphen an der x-Achse; alle übrigen Fälle ergeben sich daraus.
bewirkt eine Spiegelung des Graphen an der x-Achse; alle übrigen Fälle ergeben sich daraus.
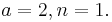
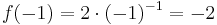 und
und